Schriftliches Dividieren ist das heutige Thema. Diese Methode hilft Dir dabei, große Zahlen auf dem Papier zu teilen. Du lernst dies zunächst für den Fall ohne Rest. Danach zeige ich Dir, wie man mithilfe derselben Methode auch die Division mit Rest durchführen kann. Als etwas fortschrittlicheres Thema findest Du zudem weiter unten, wie Du Kommazahlen dividieren kannst. Als Grundlage für schriftliches Dividieren mit und ohne Rest solltest Du dabei das Einmaleins beherrschen. Ebenso solltest Du schriftlich subtrahieren können. All diese Grundlagen zeigen wir Dir zudem ausführlich in unserer Mathe Nachhilfe. Lass uns loslegen!

Inhaltsverzeichnis
- Schriftliches Dividieren oder auch teilen
- Teilen mit Rest – Schriftlich dividieren
- Schriftliche Division Erklärung
- Ein Beispiel: Teilen mit großen Zahlen
- Schriftlich dividieren mit Rest
- Schriftliches Dividieren mit Komma – nicht periodisch
- Schriftlich teilen mit Komma – periodisch
- Schriftlich dividieren Aufgaben mit Lösungen
- Literatur
- FAQs zum Dividieren
Schriftliches Dividieren oder auch teilen
Schriftliches Dividieren gehört zu den vier Grundrechenarten. Zum Dividieren oder auch „Teilen“ teilst Du eine große Zahl (den Dividenden) durch einen Divisor (auch Teiler genannt) und erhältst das Ergebnis (den Quotienten).
28 : 4 = 7
Dividend Divisor (Teiler) Quotient
Gerade bei Divisionsaufgaben, bei denen der Dividend weit über das kleine Einmaleins hinaus geht, ist diese Art des Teilens sinnvoll und bringt Dich dabei schnell zur Lösung. Zudem solltest Du kleine Divisionsaufgaben lösen können, damit Du gut schriftlich dividieren kannst.
Hintergründe, warum schriftliches Dividieren wichtig ist, sowie weitere Einzelheiten, findest Du beispielsweise auf der Seite der Universität Landau. Aber auch in unserer Hausaufgabenbetreuung findest Du viele Informationen und Übungen zum schriftlichen Dividieren.
Teilen mit Rest – Schriftlich Dividieren
Um schriftliches Dividieren zu verstehen, möchte ich Dir kurz das Teilen mit Rest in Erinnerung rufen.
Fangen wir mit einer einfachen Division an, beispielsweise 10 : 5. Du weißt sicher, dass das Ergebnis gleich 2 ist, da die 5 genau zweimal in die 10 passt.
Weil sie aber auch genau zweimal in die 10 passt, bleibt hier kein Rest. Anders sieht es z.B. bei 11 : 5 aus. Diese Division geht nicht auf, aber da Du bereits weißt, dass die 5 zweimal in die 10 passt, können wir sagen, dass sie auch zweimal in die 11 passt.
Geht eine Division also nicht auf, kannst Du das Ergebnis trotzdem als Division mit Rest angeben.
Also: 11 : 5 = 2 Rest 1
Halbschriftliche Division
Oft kannst Du große Zahlen teilen, ohne schriftlich dividieren zu müssen, sondern mit einfachen Beobachtungen und Vereinfachungen. Nehmen wir dabei als Beispiel 192 : 6.
Zuerst suchst Du eine kleinere Zahl als 192, welche ein einfaches Vielfaches von 6 ist. Da du 3 • 6 =18 sicher im Kopf hast, eignet sich die 180 gut, denn die 6 passt hier 30 mal rein! Bleiben also bei 192 – 180 = 12 übrig. Hier passt die 6 zweimal rein und da 30 + 2 = 32 ist, hast Du Dein Ergebnis!
Es gilt also: 192 : 6 = 32
Schriftliche Division Erklärung
Schriftliches Dividieren basiert darauf, dass Du den (großen) Dividenden Schritt für Schritt durch den Teiler teilst, bis Du das gewünschte Ergebnis hast (vgl. Schipper/ Dröge/Ebeling (2000)). Dabei geht dies am einfachsten mithilfe des folgenden Schemas. Ich zeige es Dir an einem Beispiel.
Ein Beispiel: Teilen mit großen Zahlen
Nun empfehlen wir Dir, Dich mit unserem Themenbereich Schriftliches Multiplizieren vertraut zu machen. Schreibe zunächst die Divisionsaufgabe auf und lasse unterhalb des Dividenden sowie rechts vom Gleichheitszeichen genug Platz. Dabei ist das Teilen nun eine Wiederholung der folgenden vier Schritte.
Wir nehmen als Beispiel: 5752 : 3
- Teile die erste Ziffer des Dividenden durch den Teiler (siehe orangefarbener Pfeil). Da die Division 5 : 3 nicht aufgeht, führen wir eine Division mit Rest durch. Es ist 5 : 3 = 1 Rest 2. Wir notieren dabei die 1 rechts vom Gleichheitszeichen.
- Nun multipliziere die 1 mit der 3 (grüner Pfeil) und schreibe das Ergebnis 3 unterhalb der 5, durch welche wir als erstes geteilt haben.
- Nun subtrahiere die erste Ziffer des Dividenden mit dem Ergebnis der Multiplikation.
- Im vierten Schritt verschiebst schließlich Du die nächste Ziffer des Dividenden nach unten rechts neben das Ergebnis der Subtraktion (blau).
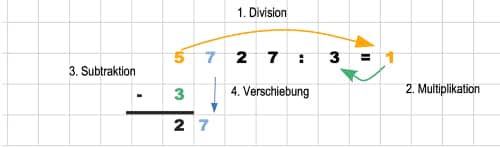
Die Zahl 27 ist nun Dein neuer Ausgangspunkt. Von ihr ausgehend wiederholst Du die obigen 4 Schritte nun bis zur letzten Ziffer des Dividenden.
Die erste Wiederholung sollte so aussehen:

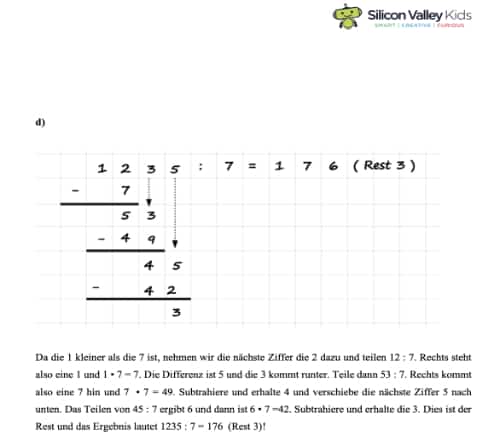
An dieser Stelle musst Du etwas vorsichtig sein! Da die 2 kleiner als die 3 ist, passt sie null Mal in die 3. Demzufolge notierst Du neben der 9 eine Null. Die übrigen Schritte sehen nun wie folgt aus:

Damit haben wir unser Ergebnis: Es gilt 5727 : 3 = 1909!
Auf der Website der Universität Kassel findest Du weitere hervorragende Erklärungen und Videos für schriftliches Dividieren.
Ein kleiner Sonderfall
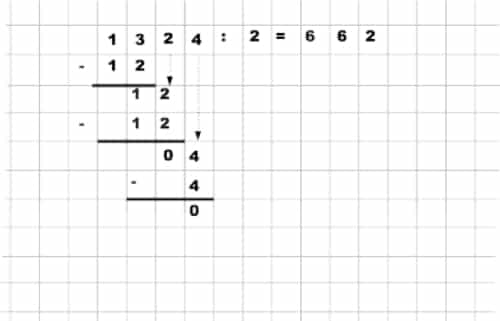
Es kann vorkommen, dass die erste Ziffer des Dividenden kleiner als der Teiler ist. Nehmen wir als Beispiel 123:3. Dabei ist hier die 1 kleiner als die 3. Dann nimmst Du einfach die nächste Ziffer dazu, fängst also mit 12 :3 an!
Achtung! Ist die erste Ziffer des Dividenden zu klein, so nimmst Du die nächste Ziffer hinzu und teilst dann diese Zahl durch den Teiler.
Hier noch ein vollständiges Beispiel für den Sonderfall:
Im Nachfolgenden siehst Du noch einmal die vier Schritte der schriftlichen Division für den Sonderfall, dass der erste Faktor der Division kleiner als der Divisor ist, aufgelistet.
1. Die erste Ziffer des Dividenden teilst Du durch den Teiler. Ist sie zu klein, nimmst Du die nächste Ziffer des Dividenden dazu. Schreibe das Ergebnis anschließend rechts neben das Gleichheitszeichen
2. Multipliziere das Ergebnis mit dem Teiler und schreibe das Produkt unter die Ziffer, welche Du im ersten Schritt geteilt hast.
3. Subtrahiere die Zahlen aus Schritt 1) und 2)
4. Verschiebe schließlich die nächste Ziffer des Dividenden nach unten neben das Ergebnis der Subtraktion .
Wiederhole nun alle Schritte bis zur letzten Ziffer des Dividenden!
Für die schriftliche Division teilst Du einzelne Ziffern des Dividenden nacheinander durch den Teiler. Dabei führst Du die 4 Schritte „teilen, multiplizieren, subtrahieren und verschieben“ nacheinander aus. Dann wiederholst Du diese vier Schritte bis zur letzten Ziffer des Dividenden. Diese Methode hilft Dir ebenso, schriftlich mit Rest zu dividieren oder auch die schriftlichen Kommazahlen zu teilen.
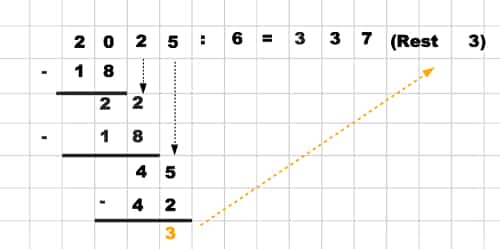
Schriftlich dividieren mit Rest
Das obige Schema der schriftlichen Division liefert Dir auch den gewünschten Rest, falls die Division nicht aufgeht. Sie ist nämlich gleich der letzten Ziffer unten, welche bisher immer die Null war:
Schriftliches Dividieren mit Komma – nicht periodisch
Das Schöne an der obigen Methode für schriftliches Dividieren ist, dass Du auch die schriftliche Division mit Kommazahlen einfach durchführen kannst.
Hier gibt es zwei Regeln zu beachten
- Kommst Du beim Komma des Dividenden an, so setzt Du auch im Ergebnis das Komma.
- Du rechnest, bist Du den Rest 0 erhältst. Bist Du bei der letzten Ziffer des Dividenden nicht fertig, so ergänzt Du eine Null.
Beispiel: Division mit Komma – nicht periodisch
Wir schauen uns das am Beispiel 12,6 : 8 an:
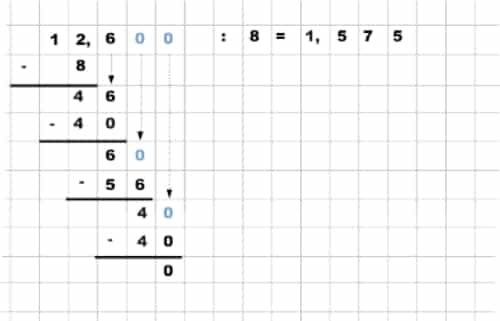
Schriftlich teilen mit Komma – periodisch
Da Du bei der Division mit Komma erst aufhörst, wenn Du bei der Null angelangt bist, kann es sein, dass Du in eine Schleife gerätst. In diesem Fall ist das Ergebnis periodisch. Sobald Du die Schleife erkennst, kannst Du die Periode im Ergebnis eintragen (vgl. Bartnitzky, H/ Brügelmann, H (2009)). Dabei nehmen wir das Beispiel 687 : 11
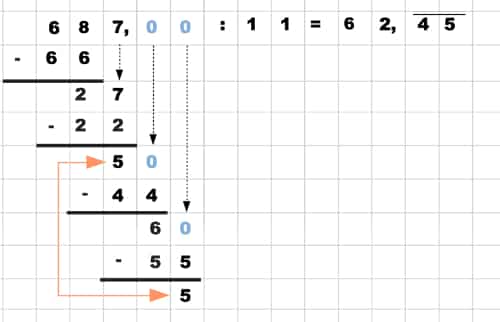
Da die Zahl 5 (siehe orangefarbener Pfeil) wieder als Ergebnis in der Subtraktion auftaucht, werden sich die Teilergebnisse wiederholen. Also bekommst Du im Ergebnis hinter dem Komma die Periode 45. Denke auch daran, das Komma zu setzen, sobald Du beim Komma des Dividenden angelangt bist.
Tabelle 1: Schriftliches Dividieren – eine Übersicht
| Verfahren | Beispiel | Bemerkungen |
| Schriftliches Dividieren mit und ohne Rest | 88 : 4 = 22 oder 99 : 8 = 12 Rest 3 | Allgemeines dividieren. Die letzte Zahl in der Rechnung gibt dabei den Rest an. |
| Schriftliches Dividieren mit Komma (nicht periodisch) | 77,5 : 5 = 15,5 | Analog zum schriftlichen Dividieren. Wird das Komma erreicht, so kommt auch im Ergebnis ein Komma. |
| Schriftliches Dividieren mit Komma (periodisch) | 10 : 3 = 3,33.. | Wird eine Schleife erreicht, so ergibt dies die Periode. |
Übrigens! Für Unternehmen bieten wir die betriebliche Kinderbetreuung inklusive Lernförderung im Fach Mathematik an.
Schriftlich dividieren Aufgaben mit Lösungen
Nun bist Du mit wertvollem Wissen für das schriftliche Teilen ausgestattet und kannst die Theorie nun auch gleich in die Praxis anwenden. Wir haben für Dich das Arbeitsblatt schriftliche Division erstellt, damit Du das Gelernte direkt üben kannst. Natürlich stellen wir Dir auch die Lösungen der Divisionsaufgaben mit ausführlicher Erklärung und Lösungsweg zur Verfügung.
Schriftlich teilen bedeutet, dass Du die einzelnen Ziffern des Dividenden nacheinander durch den Teiler teilst. Dabei führst Du die obigen vier Schritte „teilen, multiplizieren, subtrahieren und verschieben“ nacheinander aus. Dann wiederholst Du diese vier Schritte bis zur letzten Ziffer des Dividenden. Diese Methode hilft Dir ebenso schriftlich mit Rest zu dividieren oder auch schriftlich die Kommazahlen zu teilen. Probiere Dich jetzt gleich an unseren Aufgaben zum Dividieren! Zudem bist Du herzlich eingeladen, Deine Kenntnisse im Bereich schriftliches Addieren aufzufrischen.
Literatur
Schipper, W./ Dröge, R. / Ebeling, A. (2000): Handbuch für den Mathematikunterricht. 4. Schuljahr. Hannover:
Bartnitzky, H/ Brügelmann, H (2009): Kursbuch Grundschule, Frankfurt a.M.: Grundschulverband.
FAQs zum Dividieren
Die schriftliche Division hilft Dir einerseits große Zahlen zu teilen, andererseits kann diese Art des Dividierens Dir helfen, auch mit Rest oder mit Komma teilen. Außerdem wird Dir später noch die Polynomdivision begegnen, welche auf der schriftlichen Division aufbaut.
Zum schriftlichen Dividieren brauchst du eine gute Kenntnis des Einmaleins, sowie des Teilens kleinerer Zahlen mit Rest. Zudem ist es von Vorteil, wenn Du im Subtrahieren sicher bist. Unsere frühkindliche Bildung ist übrigens auch eine ideale Vorbereitung.
Genauso, nur musst Du darauf achten, dass wie beim gewöhnlichen schriftlichen dividieren der Teiler kleiner ist als die Ziffern des Dividenden. Falls nicht, musst du weitere Ziffern hinzunehmen.
Für schriftliches Dividieren gibt es eine einfache Probe. Dazu musst Du nur Dein Ergebnis mit dem Teiler Multiplizieren. Kommt hier der Dividend raus, hast Du richtig gerechnet!
Sicherlich kannst Du auch einen Taschenrechner benutzen, statt die Division auf diese Weise durchzuführen. Aber in der Mathematik ist es auch wichtig, ganze Verfahren zu lernen und möglichst fehlerfrei rechnen zu können. Außerdem ist es für das Kopfrechnen üben sowie für das kleine Einmaleins elementar. Sieh es zudem sportlich und probiere Dich, darin auch mal schneller zu werden!