Wenn Du Brüche addieren möchtest, kann Dir das Teilen und Malnehmen dabei helfen, geschickt zu rechnen. Dennoch ist die Addition von Brüchen ein bisschen anders. Um Bruchzahlen zusammenzuzählen, musst Du sie nämlich häufig erst erweitern oder kürzen und dabei teilst Du die Zähler und Nenner oder nimmst sie mal. Solltest Du dabei noch Unterstützung benötigen, zeigen wir Dir in unserer Mathe Nachhilfe alle wichtigen Regeln.
Inhaltsverzeichnis
- Wann muss man Brüche addieren?
- Addieren von Brüchen mithilfe der Streifentafel
- Gleichnamige Brüche addieren
- Rechengesetze
- Addition von Brüchen – Bruchzahlen gleichnamig machen
- Gemeinsamen Nenner finden und Bruch addieren
- Hauptnenner durch Erweitern bilden
- Gemeinsamen Nenner ermitteln und Brüche Plus rechnen
- Hauptnenner durch Kürzen bilden
- Ungleichnamige Brüche addieren
- Brüche mit ganzen Zahlen addieren
- Dezimalbruch addieren
- Gemischte Brüche addieren
- Übersicht zur Addition von Brüchen
- Übungsaufgaben zur Wiederholung
- Literatur
- FAQs – Brüche addieren
Wann muss man Brüche addieren?
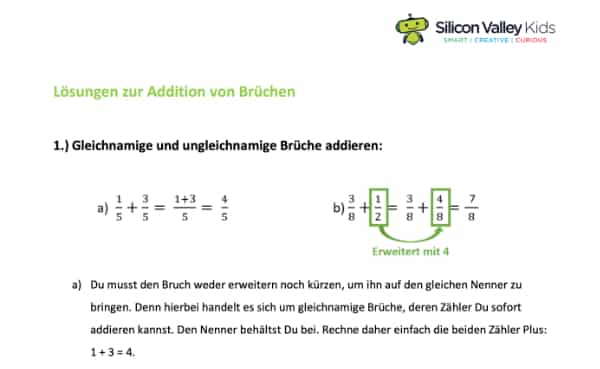
Du musst immer dann Brüche addieren, wenn Du Anteile zusammenfassen möchtest. Stell Dir vor, dass Du eine Fruchtsaftmischung aus zwei verschiedenen Säften mischen möchtest. Hierfür wählst Du Liter Bananensaft und zudem
Liter Kirschsaft, um einen Kirsch-Bananen-Saft zu mixen. Weil Du den Saft anschließend mit Deinen beiden Freunden teilen willst, musst Du wissen, wie viel Liter Du insgesamt erhältst. Auf der Abbildung siehst Du, wie man die beiden Anteile an Kirsch- und Bananensaft addieren kann. Du hast noch Probleme mit den Grundlagen? Dann wiederhole, wie schriftliches Dividieren funktioniert.
Denkst Du, dass es für drei Gläser Saft reicht?
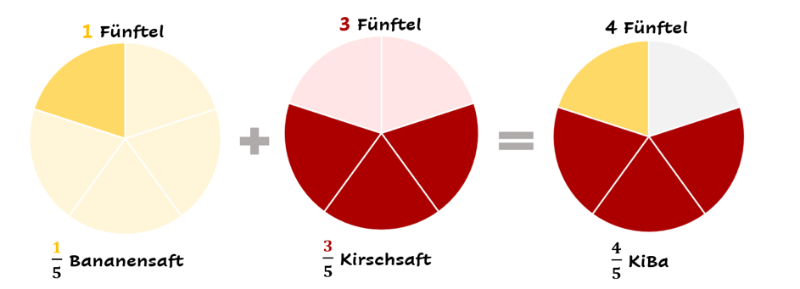
Abb. 1: Brüche addieren – Zusammenzählen von zwei Saftanteilen
Da Liter genau 1 Liter sind, reichen unsere
Liter für drei Kinder aus.
Merke:
Brüche mit demselben Nenner nennt man gleichnamige Brüche: und
sind gleichnamig.
Wie Du diese Bruchaufgabe rechnerisch lösen kannst, erklärte ich Dir noch genauer. Hast Du schon eine Rechenregel erkannt? Doch Vorsicht, nicht immer ist das Addieren von Brüchen sofort möglich. Bei unserem Beispiel konnten wir gleich addieren, weil die Nenner gleich waren. Bevor Du mit der Addition von Brüchen beginnst, solltest Du die Grundrechenarten beherrschen. Falls Du in diesem Bereich noch Probleme hast, dann schau nach, wie schriftliches Multiplizieren funktioniert.
Addieren von Brüchen mithilfe der Streifentafel
Bevor wir nun mit dem Addieren von Brüchen starten, möchte ich Dir noch eine Darstellung mit Streifenbildern zeigen. Erfahrungsgemäß helfen Streifentafeln Schülern dabei, die Bruchteile zusammenzufassen und den Rechenweg besser zu verstehen (vgl. Prediger et al., 2017). Ein weiteres Beispiel mit einer Darstellung in Streifenbildern kannst Du Dir außerdem in einer Veröffentlichung der Universität Dortmund anschauen.

Diesmal nehmen wir allerdings Bananensaft und
Kirschsaft für unser Getränk und addieren die Anteile mithilfe der Streifentafel.
Abb. 2: Mithilfe von Streifenbildern Brüche addieren
Bei diesem Beispiel erhalten wir beim Zusammenfügen von Liter Bananensaft und
Liter Kirschsaft letztendlich
Liter Saftschorle. Auch diese Menge reicht für 3 Freunde, da
Liter genau 1 Liter wäre.
Gleichnamige Brüche addieren
Bestimmt hast Du bei unseren Beispielen mit dem Kirsch-Bananen-Saft bereits eine Rechenregel erkannt. Denn bei diesen Bruchzahlen hatten wir den gleichen Nenner, nämlich die 5. Da wir sogenannte „gleichnamige Brüche“ hatten, durften wir die Zähler sofort zusammenzählen. Hierfür haben wir einfach die beiden Zähler 1 und 3 addiert und den Nenner 5 behalten.
Aufgabe:
Auch bei unserem zweiten Beispiel sind wir so vorgegangen, da wir auch hier zwei gleichnamige Brüche hatten.
Aufgabe:
Beide Bruchzahlen haben die 8 als gemeinsamen Nenner, daher dürfen wir die Zähler 3 und 4 einfach addieren und erhalten somit .
Merke:
Brüche mit gleichen Nennern addierst Du, indem Du ihre Zähler Plus rechnest. Der Nenner bleibt dabei erhalten.
Bei ungleichnamigen Brüchen musst Du jedoch vorsichtig sein, denn hier darfst Du diese Regeln nicht sofort anwenden. Ungleichnamig sind Brüche, die unterschiedliche Nenner haben, zum Beispiel und
. Wie Du in diesem Fall vorgehen kannst, erläutere ich Dir anschließend nochmal genauer. Wenn Du in Mathe auf dem Laufenden bleiben willst, dann sieh Dir doch mal unser Homeschooling Angebot an.
Rechengesetze
Wenn Du Brüche addieren möchtest, kannst Du Dir in bestimmten Fällen das Kommutativgesetz (Vertauschungsgesetz) und das Assoziativgesetz (Verbindungsgesetz) zu Hilfe nehmen. Das Kommutativgesetz (Vertauschungsgesetz) besagt, dass der Wert einer Summe sich nicht ändert, wenn die Reihenfolge der Summanden vertauscht wird (vgl. Krauthausen, 2006). Das bedeutet, dass 1 + 3 = 4 ist und 3 + 1 = 4. Die Zahlen 1 und 3 sind die Summanden und das Ergebnis 4 bezeichnet man als Summe. Dieses Gesetz kannst Du auch auf die Bruchrechnung anwenden:
Vertauschungsgesetz: und
Das Assoziativgesetz (Verbindungsgesetz) besagt, dass man die Summanden einer Summe wie man möchte zusammenfassen darf (vgl. Krauthausen, 2006). Deswegen ist sowohl 1 + 2 + 4 = 7, aber auch

Dasselbe kannst Du beim Zusammenfassen von 3 Brüchen auch machen:
Verbindungsgesetz: und
und
Addition von Brüchen – Bruchzahlen gleichnamig machen
Dir ist bestimmt aufgefallen, dass wir bisher nur mit gleichnamigen Brüchen gerechnet haben. Außerdem hatte ich Dich bereits gewarnt, dass unsere Rechenregel nur für die Gleichnamigen, aber nicht für die Ungleichnamigen gilt. Daher wollen wir uns nun anschauen, wie man zwei ungleichnamige Brüche in zwei gleichnamige verwandeln kann. Denn erst dann kannst Du addieren.
Deshalb müssen wir uns zuerst mit dem Kürzen und Erweitern sowie dem kleinsten gemeinsamen Vielfachen (kgV) und zudem dem größten gemeinsamen Teiler (ggT) befassen. Denn das Gleichnamigmachen und das Wissen über das kgV sind wichtige Voraussetzungen für das Addieren der Brüche (vgl. Sill, 2019). Vereinfacht ausgedrückt, suchen wir den gemeinsamen Nenner der beiden Brüche, d.h. wir schauen welche Zahlen die Nenner gemeinsam haben. Wie das geht, zeige ich Dir jetzt.
Merke:
Bevor Du ungleichnamige Brüche addieren kannst, musst Du sie auf den gleichen Nenner bringen.
Gemeinsamen Nenner finden und Bruch addieren
Um die Brüche gleichnamig zu machen, musst Du zunächst den gemeinsamen Nenner der beiden Bruchzahlen finden. Erst dann kannst Du den Bruch erweitern oder kürzen. Doch was ist der gemeinsame Nenner?
Gewusst?
Den gemeinsamen Nenner nennt man auch Hauptnenner.
Der Hauptnenner ist das kleinste gemeinsame Vielfache (kgV) der einzelnen Nenner : Also die kleinste Zahl, die sowohl von dem einen als auch dem anderen Nenner ein Vielfaches ist. Demzufolge ist das kgV von 3 und 5 die 15, denn die 15 ist sowohl ein Vielfaches von 3 als auch von 5. Anders ausgedrückt, 15 ist sowohl durch 3 als auch durch 5 teilbar.
Angenommen wir haben und
, dann ist 15 der Hauptnenner der beiden Nenner 5 und 3.
Der Hauptnenner von und
ist 15.
Um sie gleichnamig zu machen, musst Du sie also auf den Nenner 15 erweitern.
Hauptnenner durch Erweitern bilden
Nachdem Du weißt, wie man das kleinste gemeinsame Vielfache (kgV) ermittelt, machen wir die beiden Brüche durch Erweitern gleichnamig. Man nennt dies auch den Hauptnenner bilden.
Merke:
Beim Erweitern musst Du Zähler und Nenner mit der gleichen Zahl malnehmen.
Allerdings nimmst Du den Zähler und Nenner nicht mit irgendeiner Zahl mal, sondern mit der Zahl, die den Hauptnenner ergibt.
Du hast herausgefunden, dass 15 der Hauptnenner von und
ist. Nun musst Du überlegen, wie oft Du die 5 malnehmen musst, um anschließend 15 zu erhalten. Das ist ganz einfach: 3-mal. Dann überlegst Du, wie oft Du den Nenner 3 von
malnehmen musst, um 15 zu erhalten. Das ist auch nicht schwer, nämlich 5-mal. Demzufolge müssen wir
mit 3 erweitern und
zudem mit 5. Dafür nehmen wir sowohl Zähler als auch Nenner mit der gleichen Zahl mal.
erweitert mit 3:
und
erweitert mit 5:
Nun kannst Du die beiden erweiterten Brüche miteinander addieren, denn sie haben 15 als gemeinsamen Hauptnenner.
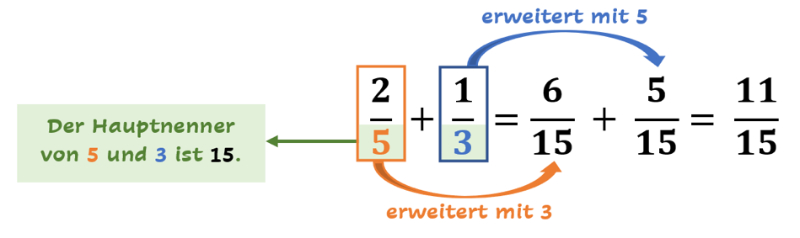
Abb. 3: Um Brüche zu addieren, musst Du den Hauptnenner bilden
Gemeinsamen Nenner ermitteln und Brüche Plus rechnen
Bisher hast Du gelernt, wie man den gemeinsamen Nenner durch das kleinste gemeinsame Vielfache ermittelt. Anschließend hast Du den Hauptnenner durch Erweitern gebildet.
Du kannst als Hauptnenner aber auch den größten gemeinsamen Teiler (ggT) von zwei Zahlen ermitteln – also die größte Zahl, durch die sich beide Zahlen teilen lassen. Dabei darf kein Rest bleiben. Demnach ist der ggT von 15 und 35 die 5, denn die 15 und die 35 sind beide durch 5 teilbar.
Nehmen wir an, dass wir mit und
rechnen wollen, dann ist 5 der Hauptnenner der beiden Nenner 15 und 35. Um die beiden Brüche gleichnamig zu machen, musst Du sie also auf den Nenner 5 kürzen.
Der Hauptnenner von und
ist 5.
Doch Achtung! Jetzt wird es ein bisschen kompliziert. Das gilt nur dann, wenn Du sowohl Zähler als auch Nenner durch die gleiche Zahl kürzen kannst!
Achtung!
Nenner und Zähler müssen durch die gleiche Zahl teilbar sein, damit der ggT Dein Hauptnenner sein kann.
Wann Du durch Kürzen einen Bruch auf den gleichen Nenner bringen darfst, erkläre ich Dir jetzt.
Hauptnenner durch Kürzen bilden
Da wir jetzt wissen, wie man den größten gemeinsamen Teiler ermittelt, machen wir die beiden Bruchzahlen durch Kürzen gleichnamig, d.h. wir bilden durch Kürzen den Hauptnenner. Das geht aber nur dann, wenn man Zähler und Nenner durch die gleiche Zahl teilen kann.
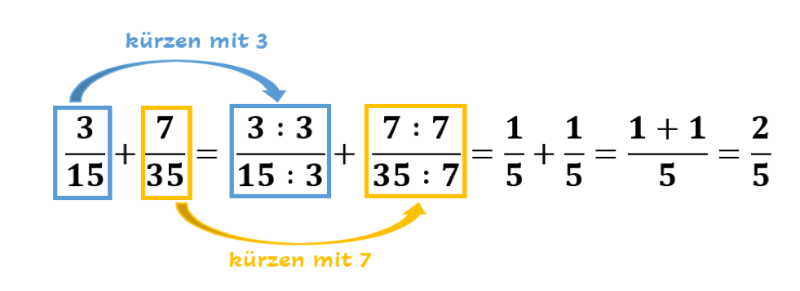
Abb. 4: Bei der Addition von Brüchen den Hauptnenner durch Kürzen bilden
Bei diesem Beispiel konnten wir wunderbar kürzen, um somit anschließend geschickt zu rechnen. Leider ist das nicht immer möglich. Deshalb zeige ich Dir nun ein Rechenbeispiel, das ungerade Zahlen enthält und bei dem es nicht möglich ist, obwohl der Hauptnenner auch 5 wäre.
Aufgabe: Hier kann der Hauptnenner nicht durch Kürzen gebildet werden.
Um beide Brüche auf den Hauptnenner 5 zu bringen, müsstest Du von sowohl den Nenner 5 als auch den Zähler 15 durch 3 teilen. Das funktioniert nur für den Nenner 15, nicht aber für den Zähler 5. Ebenso müsstest Du bei
Zähler und Nenner durch die 7 teilen. Das geht aber nicht.
Aufgabe:
Unser Hauptnenner ist die 4 und wir müssen nur den zweiten Bruch mit 5 kürzen, um den gemeinsamen Nenner zu bilden.
Ungleichnamige Brüche addieren
Obwohl Du nun weißt, wie man bei Brüchen den Hauptnenner durch Kürzen oder Erweitern ermitteln kann, wollen wir noch ein Beispiel versuchen.
Aufgabe:
Hier ist unser Hauptnenner 14. Wir bilden ihn dabei durch Erweitern. Der gemeinsame Nenner kann jedoch nicht 7 sein, weil vom zweiten Bruch nur der Nenner 14 durch 2 teilbar ist. Der Zähler 1 kann nicht durch 2 geteilt werden. Deswegen müssen wir den ersten Bruch mit 2 erweitern, um unseren Hauptnenner zu bilden. Anschließend kannst Du wie üblich weiterrechnen.
Brüche mit ganzen Zahlen addieren
Nachdem Du bereits weißt, wie man einen gemischten Bruch addieren kann, ist das Rechnen mit ganzen Zahlen sehr leicht. Wenn Du Brüche mit ganzen Zahlen addieren willst, kannst Du Dir das Plus einfach wegdenken und das Ergebnis direkt als gemischten Bruch angeben. Bei einem gemischten Bruch steht vor der Bruchzahl dabei eine ganze Zahl.
Aufgabe: und
Hierbei ist es unwichtig, ob die ganze Zahl hinter oder vor dem Pluszeichen steht. Du kannst zudem auch ganz einfach einen gemischten Bruch mit einer ganzen Zahl addieren.
Aufgabe: und
Du siehst hier, wie Du die ganze Zahl des gemischten Bruchs einfach mit der anderen gemischten Zahl zusammenzählen kannst.
Dezimalbruch addieren
Wenn Du schriftliches Addieren gut kannst, ist die Addition mit Dezimalbrüchen nicht schwierig. Beim Rechnen mit Dezimalzahlen ist es jedoch besonders wichtig, dass alle Stellen vor und hinter dem Komma korrekt untereinanderstehen.
Gewusst?
Dezimalbrüche nennt man auch Dezimalzahlen oder Kommazahlen.
Wenn Du einen Dezimalbruch addieren möchtest, gehst Du wie bei der normalen Addition vor und schreibst Deine Zahlen untereinander. Allerdings denkst Du Dir bei den Kommazahlen das Komma weg und rechnest wie gewohnt von rechts nach links.
Nachdem Du das Ergebnis berechnet hast, zählst Du die Kommastellen ab und schreibst das Komma an die richtige Stelle.
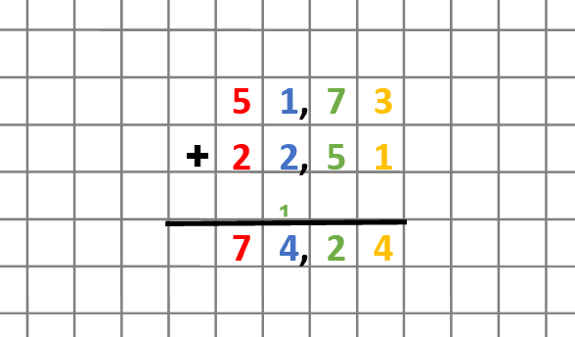
Abb. 5: Dezimalbrüche addieren
Gemischte Brüche addieren
Nun zeige ich Dir noch, wie man gemischte Brüche addieren kann. Danach solltest das Addieren von Brüchen aller Art kein Problem mehr für Dich sein. Im Grunde genommen wenden wir die gleichen Regeln wie bisher an. Jedoch müssen wir den gemischten Bruch zunächst in einen Unechten umwandeln.
Merke:
Einen gemischten Bruch wandelst Du um, indem Du Ganze Zahl Nenner + Zähler rechnest. Dein Ergebnis steht auf dem Bruchstrich und der Nenner bleibt: .
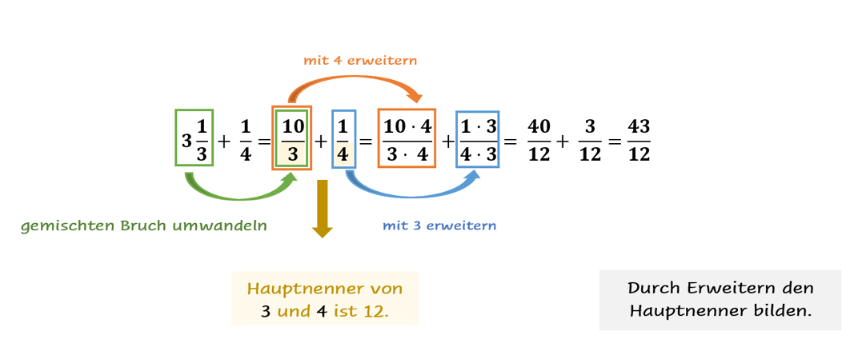
Abb. 6: Das Addieren von gemischten Brüchen
So addierst Du gemischte Brüche:
- Wandle den gemischten Bruch in einen Unechten um.
- Ermittle den gemeinsamen Nenner (Hauptnenner).
- Erweitere oder kürze entsprechend, um den Hauptnenner zu bilden.
- Nun kannst Du die beiden Zahlen miteinander addieren.
Übersicht zur Addition von Brüchen
Nun weißt Du, wie man ganz unterschiedliche Brüche addieren kann. Damit Du anschließend alle Additions-Verfahren bei der Bruchrechnung im Überblick behältst, haben wir hier eine übersichtliche Tabelle für Dich.
Tabelle 1: Eine Übersicht zum Addieren von Brüchen
| Art | Beispiel | Bemerkung |
| Gleichnamige | | Zähler der gleichnamigen Brüche Plus rechnen. |
| Ungleichnamige | | Brüche auf den gleichen Nenner bringen, dann die Zähler addieren. |
| Bruch und ganze Zahl | | Pluszeichen wegdenken und gemischten Bruch schreiben. |
| Dezimalbrüche | 4,5 + 5,1 = 9,6 | Schriftliche Addition durchführen und Komma setzen. |
| Gemischte Brüche | | Gemischten Bruch in unechten umwandeln. Dann gleichnamige Brüche addieren. |
Übungsaufgaben zur Wiederholung
Jetzt hast Du viel über das Addieren von Brüchen gelernt und kannst Dein Können ausprobieren. Damit Du fleißig üben kannst, haben wir Dir ein paar Übungsaufgaben mit Lösungen bereitgestellt. Wir wünschen viel Spaß beim Lösen! Du hast noch nicht genug von Bruchzahlen? Dann schau nach, wie man Brüche dividieren kann.
Die Addition der Brüche ist gar nicht schwierig. Nachdem Du den gemeinsamen Nenner der Bruchzahlen gefunden hast, kannst Du die Zähler einfach addieren. Jetzt weißt Du sogar, wie man mit ungleichnamigen Brüchen und Dezimalbrüchen rechnet oder einen Bruch mit einer ganzen Zahl zusammenzählt. Falls Du noch Fragen hast, helfen wir Dir gern in unserer Hausaufgabenbetreuung weiter. Du kannst die Addition schon gut? Dann lerne als nächstes, wie man Brüche subtrahieren kann.
Literatur
Krauthausen, G., Scherer, P. (2006): Einführung in die Mathematikdidaktik. Heidelberg: Elsevier Spektrum Akademischer Verlag.
Prediger, S., Glade, M., Schmidt, U. (2011): Wozu rechnen wir mit Anteilen? – Herausforderungen der Sinnstiftung am schwierigen Beispiel der Bruchoperationen. Praxis der Mathematik in der Schule, 52(37), pp. 28-35.
Sill, H.-D. (2019): Grundkurs Mathematikdidaktik. Paderborn: Ferdinand Schöningh.
FAQs – Brüche addieren
Besonders dann, wenn Du die Brüche auf den gleichen Nenner bringen musst, wird die Kopfrechnung schwierig. Aber probiere es doch einfach mal aus, denn dabei kannst Du gleichzeitig Kopfrechnen üben.
Falls Du Brüche Minus rechnen möchtest, musst Du wieder gemeinsamen Nenner der Bruchzahlen finden. Anschließend rechnest Du die Zähler Minus. Schriftliches Subtrahieren von Brüchen ist daher genauso leicht wie das Addieren: .
Das Addieren von drei Brüchen ist auch möglich. Hierfür musst Du den gemeinsamen Nenner finden und sie dementsprechend erweitern oder kürzen. Anschließend führst Du wie gewohnt die Addition von Brüchen durch: .
Manchmal muss man auch mehr als 3 Brüche addieren. Wenn Du einen großen gemeinsamen Nenner bekommst, kann dies schwierig werden. Das Ergebnis muss Du dann unbedingt wieder kürzen: .
Wenn sie gleich sind, kannst Du Brüche multiplizieren, statt sie zu addieren: oder
.