Symmetrie ist ein Merkmal einiger geometrischer Objekte. Man nennt ein Objekt symmetrisch, wenn Du es zum Beispiel spiegeln kannst und es danach auf sich abgebildet werden kann. Wie genau das funktioniert, erklären wir Dir hier. Außerdem zeigen wir Dir, welche vier Arten dieses Phänomens es gibt und wie Du sie erkennst. Wenn Du noch etwas Hilfe möchtest, dann bekommst Du in unserer Mathe Nachhilfe nochmal eine ausführliche Erklärung.

Was ist Symmetrie?
Symmetrie ist eine Eigenschaft einiger geometrischer Objekte, wie zum Beispiel von Quadraten. Dabei können sie durch Spiegelung, Drehung oder Verschiebung unverändert auf sich selbst abgebildet werden. Du fragst Dich, was genau damit gemeint ist? Schauen wir uns doch mal ein Beispiel dazu an:
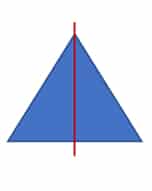
Das Dreieck haben wir an der roten Linie gespiegelt. Es sieht auf der linken Seite genauso aus, wie auf der rechten. Wenn Du es an der Linie zusammenfalten würdest, würden die Teile außerdem genau übereinander passen. Das Dreieck ist also symmetrisch. Das funktioniert aber nicht nur mit einer Figur. Es können nämlich auch zwei geometrische Figuren symmetrisch zueinander sein. Das siehst Du an unserem zweiten Beispiel:
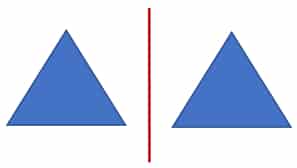
Wenn Du das eine Dreieck an der roten Linie spiegelst, dann würde es genau auf dem anderen Dreieck abgebildet werden. Anders gesagt: Du könntest das Papier an der Linie falten und beide Dreiecke würden exakt übereinander liegen. Das liegt daran, dass beide Dreiecke nicht nur gleich geformt sind, sondern auch den gleichen Abstand zur Achse haben. Insgesamt gibt es vier verschiedene Symmetrie-Arten. Welche Besonderheiten sie haben, ist in der Tabelle zusammengefasst.
Tabelle 1: Überblick über die 4 Symmetrie-Arten
| Art | Spiegelung | Besonderheit |
| Achsensymmetrie | An einer Achse | Gleiche Abbildung der Figur |
| Punktsymmetrie | An einem Punkt | Figur steht auf dem Kopf |
| Drehsymmetrie | Durch Drehung | Figur dreht sich |
| Asymmetrie | Keine | Es liegt keinerlei Symmetrie vor |
Achsensymmetrie
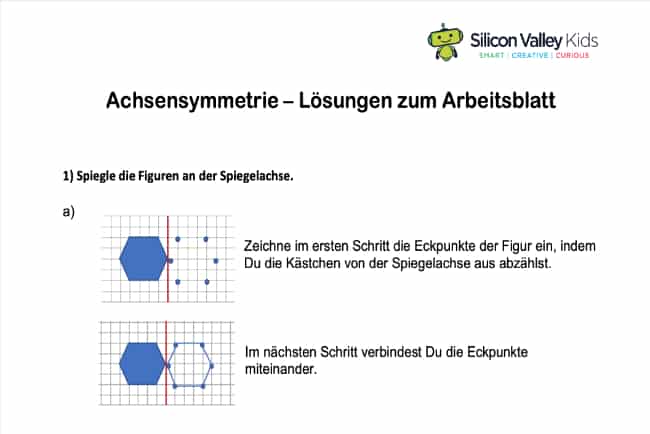
Die wichtigste Art der Symmetrie in der Grundschule ist die Achsensymmetrie (vgl. Graumann, 2002). Diese kennst Du bereits aus unserem zweiten Beispiel. Dabei spiegelt man eine geometrische Figur nämlich an einer festgelegten Linie, die auch Symmetrieachse genannt wird. Das funktioniert ganz einfach, indem man alle Punkte einer Figur mit exakt denselben Abständen auf die gegenüberliegende Seite der Achse überträgt. Lass uns hierzu ein Beispiel betrachten:
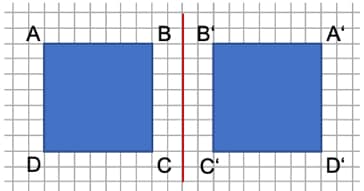
Das Quadrat wurde an der roten Achse gespiegelt. Der Eckpunkt A hat dabei genau den gleichen Abstand zur Achse wie der gespiegelte Punkt A‘ auf der gegenüberliegenden Seite. Genauso ist es auch bei den Punkten B → B‘, C → C‘ und D → D‘. Sollst Du in der Schule die Achsensymmetrie bestimmen, dann kannst Du einfach die Kästchen abzählen und auf diese Weise den Abstand ermitteln. Falls keine Kästchen vorhanden sind, kannst Du die Abstände ebenso gut mit einem Lineal abmessen.
Übrigens
Die Symmetrieachse wird auch Spiegelachse genannt, denn sie funktioniert im Prinzip wie ein solcher. Auch ein Spiegel bildet nämlich eine Form genau symmetrisch ab.
Da du jetzt die Achsensymmetrie kennst, kann es gleich mit dem praktischen Teil weitergehen. Mit unserem Arbeitsblatt kannst Du selber zum Stift greifen und mit dem Üben beginnen. Viel Spaß dabei!
Punktsymmetrie
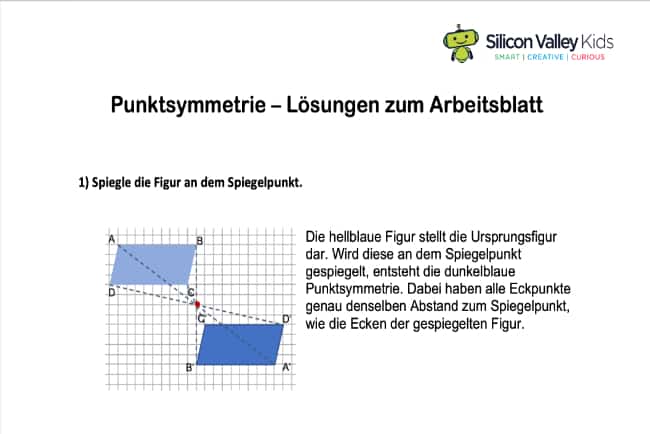
Bei der Punktsymmetrie gibt es keine Spiegelachse, sondern die Spiegelung findet an einem bestimmten Punkt statt (vgl. Gernth/Rose, 1997). Das wird mit diesem Beispiel deutlicher:
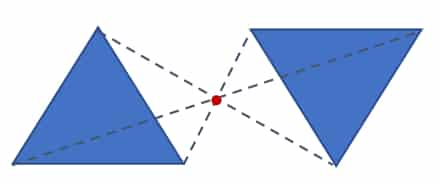
Auch hier werden alle Punkte der Figur mit demselben Abstand auf die gegenüberliegende Seite übertragen. Allerdings spiegeln wir hierbei nicht an einer Achse, sondern an einem sogenannten Spiegelpunkt. Da alle Eckpunkte den gleichen Abstand zum Spiegelpunkt haben, wie der jeweilige Ursprungspunkt, sind die beiden Dreiecke punktsymmetrisch zueinander.
Du kannst Dir merken, dass die Figur nur dann vollständig übertragen wurde, wenn sich alle Hilfslinien im Spiegelpunkt kreuzen. Dann kann die Figur nach der Spiegelung vollständig auf sich selbst abgebildet werden. Eine weitere Eigenschaft der Punktspiegelung ist außerdem, dass die Figur nach der Spiegelung auf dem Kopf steht und somit eine 180°-Drehung stattgefunden hat.
Unser Tipp
Übertrage immer zuerst die Eckpunkte der Figur und verbinde sie danach miteinander. Auf diese Weise erhältst Du ganz einfach die Spiegelung der Figur.
Hast Du alles verstanden? Sehr gut gemacht! Dann bist du ja bestens auf unser Übungsblatt vorbereitet!
Seltene Variante – Drehsymmetrie
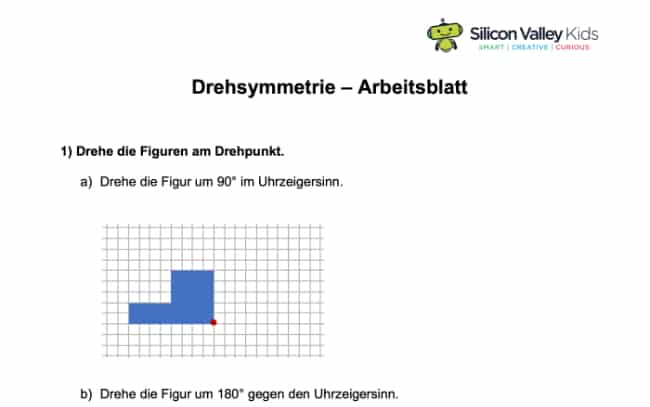
Bei der Drehsymmetrie orientieren wir uns ebenfalls an einem festen Punkt. Wie der Name Dir bestimmt schon verrät, wird bei dieser Variante um einen Punkt gedreht statt gespiegelt. Man kann die Figuren dabei um eine bestimmte Gradzahl rotieren. In unserem Beispiel wird das Quadrat zweimal um 90° gedreht:
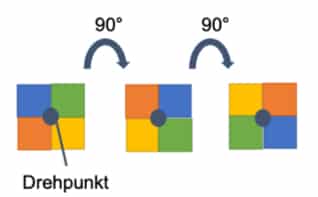
Damit Du die Drehung besser sehen kannst, haben wir Dir die vier Ecken bunt eingefärbt. Da der Drehpunkt sich innerhalb der Figur befindet, dreht sie sich um sich selbst. Der Punkt kann aber auch außerhalb der Figur liegen. Generell gilt aber: Bei der Rotation verändern sich alle Punkte der Figur um dieselbe Gradzahl.
Übrigens
Wird eine Figur um 180° gedreht, dann steht sie auf dem Kopf und Du erhältst eine Punktsymmetrie. Deshalb gilt diese Art zudem als eine Form der Drehsymmetrie.
Das war nun schon etwas schwerer, oder? Mit dem Arbeitsblatt kannst Du prüfen, ob Du alles verstanden hast. Falls Du mal nicht weiterkommst, dann kann Dir das Lösungsblatt helfen.
Asymmetrie
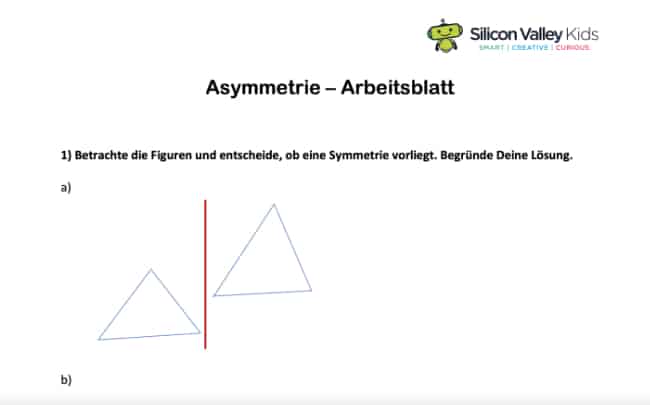
Bei einer Asymmetrie liegt keinerlei Symmetrie vor. Das bedeutet, dass die Figur weder achsensymmetrisch, punktsymmetrisch noch drehsymmetrisch ist. Unser Beispiel zeigt Dir, wie genau das aussehen kann:
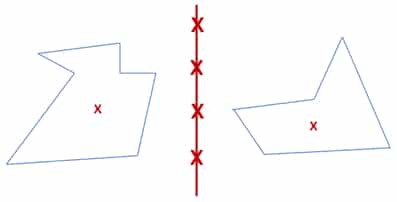
Wie Du bestimmt erkennen kannst, lässt sich die linke Figur nicht exakt auf die rechte abbilden. Damit liegt keine Spiegelung vor. Außerdem sind beide Figuren nicht in sich symmetrisch. Wenn man sie nämlich in der Mitte faltet, dann liegen nicht alle Kanten aufeinander.
Die Asymmetrie zu erkennen, kannst Du gleich mit unseren Übungsaufgaben trainieren. Solche Aufgaben sind übrigens auch super für das Homeschooling geeignet. Also, worauf wartest Du noch? Schnapp‘ Dir das Aufgabenblatt und los geht’s!
Der Geometrieunterricht ist laut der Universität Potsdam von großer Bedeutung. Dabei sind Symmetrien ein wichtiger Bestandteil und sie begegnen Dir auch im Alltag ständig. Nun ist es aber bestimmt kein Problem für Dich, die unterschiedlichen Arten auseinanderzuhalten. Wenn Du noch mehr Aufgaben zum Üben möchtest oder Fragen hast, hilft unsere Hausaufgabenbetreuung Dir weiter.
Literatur
Gernth, Ulrich; Rose, Friedrich-Wilhelm (1997): Mathematik, 5. und 6. Klasse. Geometrie: Symmetrie, Kreis, Winkel, Rowohlt Tb., S. 95.
Graumann, Günter (2002): Mathematikunterricht in der Grundschule: Studientexte zur Grundschulpädagogik und -didaktik, Bad Heilbrunn/Obb: Klinkhardt.
FAQs – Symmetrie
Eine symmetrische Figur kann durch Spiegelung, Drehung oder Verschiebung auf sich selbst abgebildet werden und erscheint somit unverändert.
Figuren können auch an mehreren Achsen gespiegelt werden und bleiben dabei symmetrisch. Bei einem Kreis lassen sich sogar endlos viele Spiegelachsen finden!
Bei der ersten Form spiegelst Du die Figur entlang einer Achse, während Du sie bei der Punktsymmetrie an einem Punkt spiegelst.
Dreht man eine Figur um 180°, dann ist das Ergebnis das gleiche, wie bei der Punktsymmetrie.
Eine Figur ist asymmetrisch, wenn sie nicht genau auf sich selbst abgebildet werden kann.