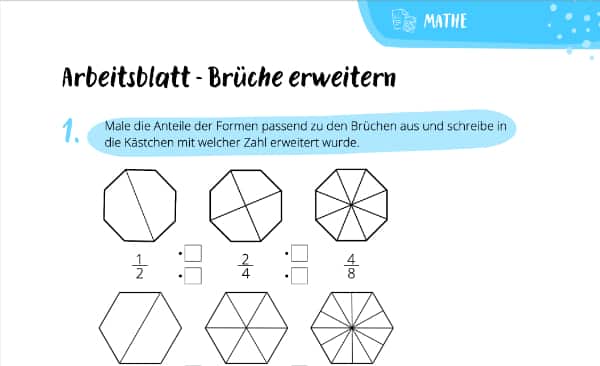
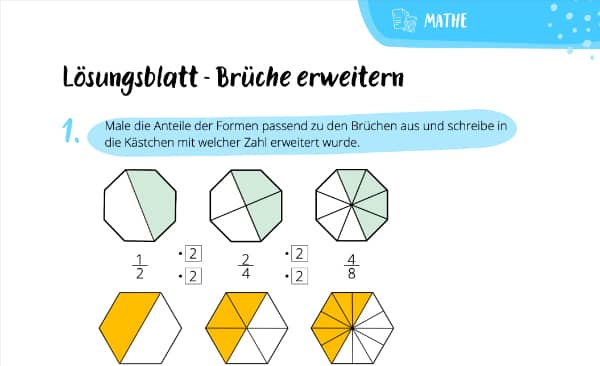
Brüche erweitern klappt, indem Du die Zahl oberhalb und unterhalb des Bruchstrichs mit der gleichen Zahl malnimmst. Manchmal ist das die einzige Möglichkeit, um weiter rechnen zu können. Alles Nötige dazu erklären wir Dir im Anschluss. Sollte es dennoch Fragen geben, ist die Mathe Nachhilfe die richtige Adresse für Dich!

Was bedeutet Brüche erweitern?
Brüche erweitern heißt, den Zähler und Nenner mit derselben Zahl zu multiplizieren. Dabei sieht die Teilmenge dann anders aus. Eigentlich versteckt sich dahinter aber die gleiche Zahl. Es ist nämlich egal, ob Du oder
schreibst. Umgeschrieben wird aus beiden 0,2.
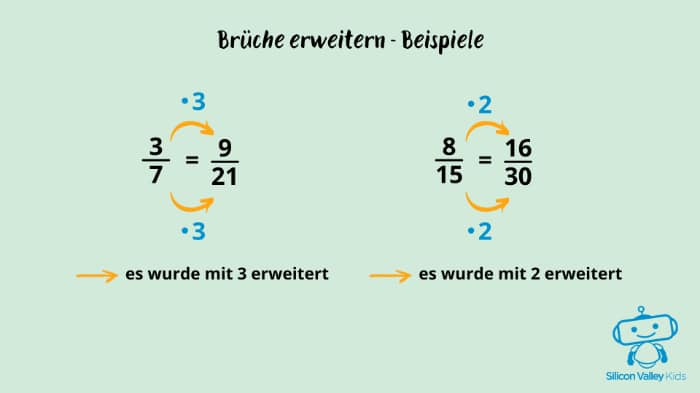
Wie erweitert man einen Bruch?
Um Brüche erweitern zu können, suchst Du Dir eine Zahl aus, mit der Du sie malnimmst. Diese Zahl heißt deswegen auch Erweiterungszahl (vgl. Klett, 2015). Anders als wenn Du Brüche kürzen möchtest, kann das theoretisch jede beliebige Zahl sein. Es kommt also auf die jeweilige Aufgabe an. Aber wieso muss man denn jetzt erweitern? Ganz einfach: Nur so darfst Du zum Beispiel zwei Brüche addieren!
Übrigens
Auch wenn Du Brüche subtrahieren sollst, müssen die Nenner gleich sein. Man sagt dazu, sie müssen einen Hauptnenner haben (vgl. Becker / Fingerhut, 2010). Das heißt für Dich: Wahrscheinlich musst Du erweitern!
Mit derselben Zahl malnehmen
Als Erweiterungszahl kannst Du im Prinzip jede beliebige Zahl verwenden. Lass uns als Beispiel mal mit der 3 erweitern:
Kleinstes gemeinsames Vielfaches
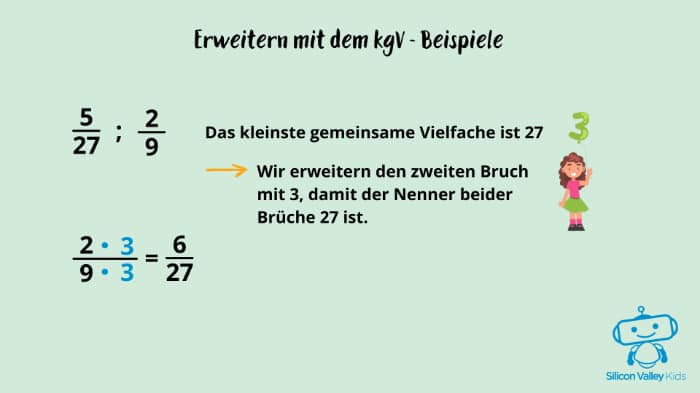
Das kleinste gemeinsame Vielfache (kgV) verwendest Du, wenn Du zwei Bruchzahlen auf einen Hauptnenner bringen sollst. Wie oben kurz erwähnt, ist das beim Addieren und Subtrahieren der Fall. Schauen wir uns folgendes Beispiel an:
Das kleinste gemeinsame Vielfache hier ist die 21, denn . Wir müssen die 7 also mit 3 multiplizieren und machen dasselbe mit der 3 im Zähler.
Das heißt für unsere Aufgabe:
Kann man jeden Bruch beliebig oft erweitern?
Du kannst so häufig mit natürlichen Zahlen erweitern, wie Du möchtest. Das würde allerdings nicht so viel Sinn ergeben. Schließlich möchtest Du Deine Aufgaben ja möglichst schnell lösen, oder? Deswegen ist es bei der Strichrechnung mit Bruchzahlen am schnellsten das kgV zu suchen. Praktisch ist das Erweitern auch, sobald Brüche vergleichen an der Reihe ist. Mit gleichnamigem Nenner fällt Kindern das laut der Universität Siegen nämlich viel leichter.
Übungen zum Erweitern von Brüchen
Bist Du bereit selbst mit Bruchzahlen zu jonglieren? Dann ist es Zeit für unser Übungsblatt! Hier kannst Du gleich testen, was Du alles gelernt hast. Falls Du aber noch Fragen hast, findest Du jederzeit Hilfe bei unserer Nachhilfe für die Grundschule.
Und schon hast Du wieder etwas Neues über die Bruchrechnung gelernt. Du weißt jetzt, wieso man manchmal erweitern muss. Außerdem konntest Du das mit den Übungsaufgaben gleich selbst ausprobieren. Das ist klasse!
Literatur
Becker, Kathrin / Fingerhut, Andrea (2010): Bruchrechnung in kleinen Schritten 3: Multiplikation und Division von Brüchen (5. bis 9. Klasse). Deutschland: Persen Verlag.
Klett (2015): Ich kann … Mathe – Brüche und Dezimalzahlen 5./6. Klasse. Deutschland: Klett Lerntraining.
FAQs – Brüche erweitern
Die Erweiterung ist nötig, sobald Du bei der Bruchrechnung addieren oder subtrahieren möchtest. Denn dafür müssen die Nenner gleich sein. Auch beim Vergleichen von mehreren Brüchen ist diese Methode eine Erleichterung.
Ja, das Erweitern funktioniert immer. Du musst nur dieselbe natürliche Zahl für den Nenner und den Zähler verwenden. Außerdem muss die Zahl größer als 1 sein, weil sich ansonsten nichts verändern würde.
Nein, der Bruchteil bleibt derselbe. Es verändert sich nur wie viele Stücke er hat. Deswegen ist genau dasselbe wie
, nämlich die Hälfte.