
Bei Kettenaufgaben müssen nacheinander mehrere Rechenschritte durchgeführt werden. Eine Aneinanderreihung von Plusaufgaben ist leicht zu lösen, bei unterschiedlichen Rechenzeichen steigt jedoch der Schwierigkeitsgrad. Einige Aufgaben können sogar ganz schön knifflig sein, da bestimmte Rechenoperationen bevorzugt behandelt werden müssen. Deshalb zeigen wir Dir in diesem Artikel, worauf Du unbedingt achten musst. Solltest Du dennoch Schwierigkeiten beim Lösen haben, dann schau in unserer Mathe Nachhilfe vorbei.
Was ist eine Kettenaufgabe?
Um Kettenaufgaben zu lösen, musst Du nacheinander mehrere Rechenoperationen durchführen. Du kannst das Ergebnis also nur ermitteln, indem Du die richtige Lösung auf alle Teilaufgaben findest. Schauen wir uns dieses Vorgehen einmal am Beispiel des Addierens an:
Aufgabe:
5 + 2 + 7 + 3 + = 17
Ebenso kann man Zahlen nacheinander Mal rechnen und auf diese Weise eine lange Aufgabe bilden:
Aufgabe:
1 ∙ 4 ∙ 3 ∙ 2 = 24
Beim Malnehmen und Plusrechnen kannst Du außerdem das Kommutativgesetz (Vertauschungsgesetz) anwenden und die Zahlen vertauschen (vgl. Käpnick, 2014).
Aufgaben:
5 + 2 + 7 + 3
7 + 5 + 2 + 3
2 + 3 + 5 + 7
1 ∙ 4 ∙ 3 ∙ 2
3 ∙ 2 ∙ 4 ∙ 1
4 ∙ 1 ∙ 3 ∙ 2

Aber Vorsicht! Nicht immer sind die Aufgaben so einfach zu lösen, denn bei Kettenaufgaben können alle Grundrechenarten gleichzeitig vorkommen. Sobald Du verschiedene Rechenzeichen in einer Aufgabe entdeckst, musst Du zudem bestimmte Rechengesetze beachten. Übrigens ist das wichtigste Gesetz die Punkt- vor Strichrechnung.
Merke:
Punkt- vor Strichrechnung bedeutet: Zuerst die Mal- und Geteiltaufgaben rechnen, dann die Plus- und Minusaufgaben.
Schauen wir uns hierzu gleich eine Beispielrechnung an:
Aufgabe:
10 : 2 + 4 – 7 + 3 ∙ 2 = (10 : 2) + 4 – 7 + (3 ∙ 2) = 5 + 4 – 7 + 6 = 8
Welche Teilaufgaben müssen wir zuerst berechnen? Wir wissen, dass Geteilt und Mal immer als Erstes an der Reihe sind. Somit rechnen wir erst 10 durch 2 und 3 mal 2. Durch diesen Rechenschritt bleiben anschließend nur noch die Addition und Subtraktion stehen. Unsere Aufgabe lautet nun: 5 + 4 – 7 + 6. Als Ergebnis erhalten wir schließlich die Zahl 8.
Wie berechnet man Kettenaufgaben?
Wie man Kettenaufgaben berechnet, ist dabei abhängig von den Rechenzeichen der einzelnen Teilaufgaben. Denn diese Zeichen entscheiden, welche Zahlen Du zuerst miteinander verrechnen darfst. Sobald eine Kettenaufgabe sowohl eine Punkt- als auch eine Strichrechnung enthält, musst Du nämlich das entsprechende Rechengesetz beachten. Deswegen zeigen wir Dir nun Schritt für Schritt, wie das geht.
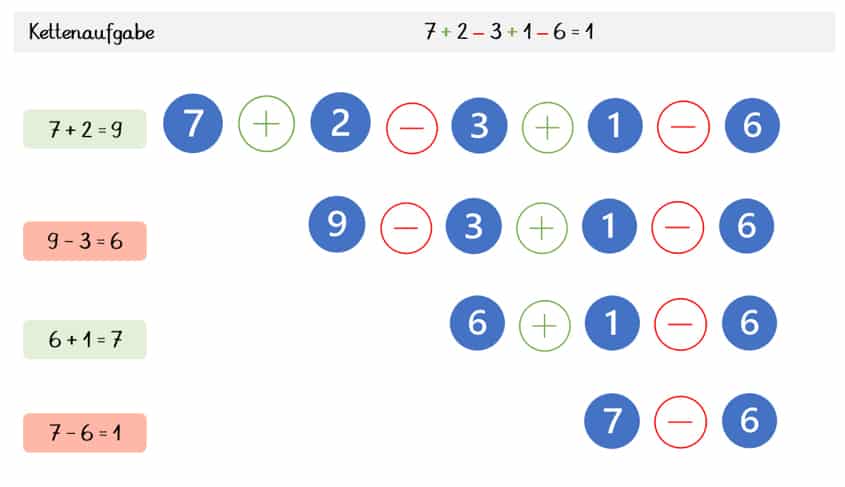
Bei dieser Aufgabe führen wir nach und nach die einzelnen Rechenoperationen durch. Wir gehen dabei von links nach rechts vor und tragen jeweils das Ergebnis der Teilaufgabe an der entsprechenden Stelle ein. Auf diese Weise wird die Kette schließlich immer kürzer.
Kurzum: Wir rechnen erst 7 + 2 = 9 und führen die Rechnung dann mit unserem Ergebnis, der Zahl 9, fort. Dadurch wird unsere ursprüngliche Aufgabe zu: 9 – 3 + 1 – 6. Anschließend rechnen wir die Teilaufgabe 9 – 3. Das Ergebnis ist 6, deshalb rechnen wir mit der Zahl 6 weiter: 6 + 1 = 7. Nun müssen wir nur noch 7 – 6 rechnen und erhalten unser Endergebnis: 1.
Bei der Addition und Subtraktion kannst Du wichtige Rechengesetze der Mathematik anwenden. Beispielsweise vereinfachen das Kommutativgesetz (Vertauschungsgesetz) und Assoziativgesetz (Verbindungsgesetz) das Rechnen (vgl. Krauthausen, 2006). Diese Gesetze erlauben Dir, die Zahlen in der Rechnung zu vertauschen oder zu verbinden:
Aufgabe:
7 + 2 – 3 + 1 – 6 oder 7 + 1 + 2 – 3 – 6
Solltest Du übrigens mehr über Rechengesetze erfahren wollen, schau Dir die Präsentationen der Universität Duisburg Essen an.
Schwieriger wird es, wenn in einer Aufgabe Plus- oder Minusrechnungen (Strichrechnungen) mit Mal- oder Geteiltrechnungen (Punktrechnungen) vermischt werden. Dann musst Du die Reihenfolge genau beachten und die Rechenregel „Punkt- vor Strichrechnung“ anwenden. Mithilfe der Klammern kannst Du sehen, wo sich eine Strichrechnung befindet, d.h. die Klammern ordnen Deine Rechenaufgabe.

Übungen für die 1. Klasse
Bei unseren Kettenaufgaben für die 1. Klasse musst Du Minus- und Plusaufgaben im Zahlenraum bis 20 lösen. Schriftliches Addieren und Subtrahieren kann Dir beim Berechnen der schwierigen Aufgaben helfen. Jedoch haben wir die Aufgaben so gestaltet, dass sie leicht im Kopf zu lösen sind und nur wenige Zwischenschritte benötigt werden.

Schau Dir unser tolles Arbeitsblatt mit vielen weiteren Aufgaben an:
Kettenaufgaben Klasse 2
Bei unseren Übungsaufgaben für die 2. Klasse darfst Du noch einmal die Addition, Subtraktion und Multiplikation im Zahlenraum bis 100 üben. Schriftliches Subtrahieren kann Dir beim Lösen eine gute Hilfe sein. Sieh Dir, bevor Du startest, unsere Rechenbeispiele für die 2. Klasse an. Achte beim Lösen unbedingt auf die Punkt- vor Strichrechnung und nutze Klammern als Hilfsmittel.

Alles verstanden? Dann geht es jetzt mit dem Arbeitsblatt für die 2. Klasse weiter.
Kettenaufgaben Klasse 3
Obwohl unsere Aufgaben für die 3. Klasse ebenfalls die 4 Grundrechenarten kombinieren, sind sie ein wenig schwieriger als die Übungen für die 2. Klasse. Du musst nun nämlich schon im Zahlenraum bis 1000 rechnen und zudem das große Einmalseins beherrschen. Schriftliches Multiplizieren wird Dir helfen, die schwierigen Malaufgaben zu lösen. Rechne auch hier die Multiplikationsaufgaben zuerst! Sieh Dir nochmal unser Beispiel an:
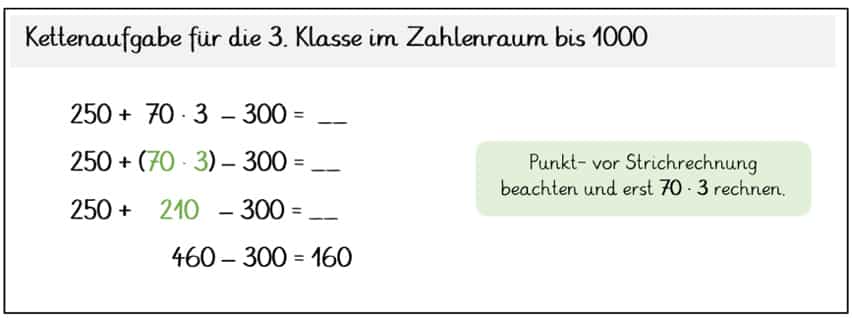
Hast Du noch Lust zu üben? Dann mach sofort mit den Aufgaben für die Klasse 3 weiter.
Arbeitsblatt für die 4. Klasse
Kettenaufgaben eignen sich hervorragend zum Üben der vier Grundrechenarten, deswegen sind sie beliebte Übungen im Mathematikunterricht der Grundschule. Bei unseren Übungsaufgaben für die 4. Klasse kommen alle 4 vor, wobei wir uns nun bereits im Zahlenraum bis 1000 bewegen. Schriftliches Dividieren hilft Dir übrigens, falls Du nicht alle Divisionsaufgaben im Kopf rechnen kannst. Beim Lösen der kniffligen Aufgaben kannst Du selbstverständlich auch alle Dir bekannten Rechentricks nutzen. Dadurch erleichterst Du Dir das Lösen.

Das Arbeitsblatt ist die perfekte Ergänzung für das Üben zu Hause und zudem für das Homeschooling geeignet. Sollten die Aufgaben jedoch zu schwierig für Dich sein, versuche Dich zunächst an den Arbeitsblättern für die Klassen 1 bis 3. Falls Du weitere Unterstützung benötigst, melde Dich bei unserer Hausaufgabenbetreuung. Viel Spaß beim Lösen der Aufgaben!
Übersicht nach Grundrechenarten
Du weißt nun, wie die Kettenaufgaben für die Klassen 1 bis 4 gelöst werden. Damit Du den Überblick behältst, haben wir zudem noch eine Tabelle mit den Rechenregeln für die einzelnen Grundrechenarten erstellt.
Tabelle 1: Rechenaufgaben mit verschiedenen Grundrechenarten
| Grundrechenart | Beispiel | Bemerkung |
| Plus (Addition) | 2 + 4 + 5 = 6 + 5 = 11 | Zahlen (Summanden) dürfen getauscht werden. |
| Minus (Subtraktion) | 20 – 2 – 8 = 18 – 8 = 10 | Die beiden Subtrahenden können getauscht werden: 20 – 8 – 2 = 10. |
| Mal (Multiplikation) | 2 ∙ 6 ∙ 1 = 12 ∙ 1 = 12 | Zahlen (Faktoren) dürfen getauscht werden. |
| Geteilt (Division) | 15 : 3 : 5 = 5 : 5 = 1 | Zahlen (Dividend und Divisoren) dürfen nicht getauscht werden. |
| Plus und Mal | 7 + 2 ∙ 3 = 7 + 6 = 13 | Punkt- vor Strichrechnung; Malaufgabe zuerst. |
| Minus und Mal | 21 – 2 ∙ 7 = 21 – 14 = 7 | Punkt- vor Strichrechnung; Malaufgabe zuerst. |
| Plus, Minus und Mal | 8 + 3 ∙ 4 – 3 = 8 + 12 – 3 = 20 – 3 = 17 | Punkt vor Strich beachten. |
| alle Grundrechenarten | 8 : 4 + 3 ∙ 7 – 5 = 2 + 21 – 5 = 23 – 5 = 18 | Punkt vor Strich; erst teilen und malnehmen, dann weiterrechnen. |
Nachdem Du jetzt ein Profi im Rechnen von Kettenaufgaben bist, kannst Du Dich einer neuen mathematischen Herausforderung stellen. Weißt Du bereits, wie man Brüche subtrahieren kann? Auch in diesem Artikel haben wir wieder viele praktische Beispiele und zudem knifflige Übungen für Dich. Falls Brüche noch zu schwierig für Dich sind, solltest Du erst ungerade Zahlen kennenlernen.
Literatur
Krauthausen, G., Scherer, P. (2006): Einführung in die Mathematikdidaktik. Heidelberg: Elsevier Spektrum Akademischer Verlag.
Käpnick, Friedhelm (2014): Mathematik lernen in der Grundschule. Heidelberg: Elsevier Spektrum Akademischer Verlag.
FAQs zum Thema Kettenaufgaben
Auch Bruchaufgaben kann man in einer Kette rechnen. Nicht zu empfehlen ist eine Aneinanderreihung jedoch beim Brüche dividieren. Denn hier sind ein paar Regeln zu beachten. Besonders einfach ist es, wenn man Brüche multiplizieren möchte:
Diese Aufgaben begegnen Dir nicht nur in der Grundschule, sondern auch in der weiterführenden Schule von der 5. Klasse bis zum Abitur.
Wahrscheinlich merkst Du manchmal gar nicht, dass Du auch im Alltag solche Aufgaben löst. Bestimmt warst Du schon einkaufen und hast Deine Ausgaben anschließend zusammengerechnet: 1,50 € + 2 € + 5 € = 8,50 €. Dabei kannst Du besonders gut das Kopfrechnen üben.
In diesen besonderen Aufgaben können verschiedene Arten von Zahlen vorkommen: Sowohl Brüche als auch ungerade und gerade Zahlen. Eine Aufgabe mit geraden Zahlen sieht dabei so aus: 2 ∙ 4 – 12 : 6 + 3 = (2 ∙ 4) – (12 : 6) + 3 = 8 – 2 + 3 = 9.
Es ist möglich, dass bei einer Textaufgabe mehrere Rechenschritte durchgeführt werden müssen. Dann ergibt sich eine längere Aufgabe, die außerdem in Text verpackt sein kann. Hier ein Beispiel: Max hat 20 €. Er kauft eine Hose für 10 €, ein Buch für 5 € und zudem ein Eis für 2 €. Außerdem findet er im Park 3 €. Wie viel Geld hat er schließlich? 20 € – 10 € – 5 € – 2 € + 3 € = 6 €.










