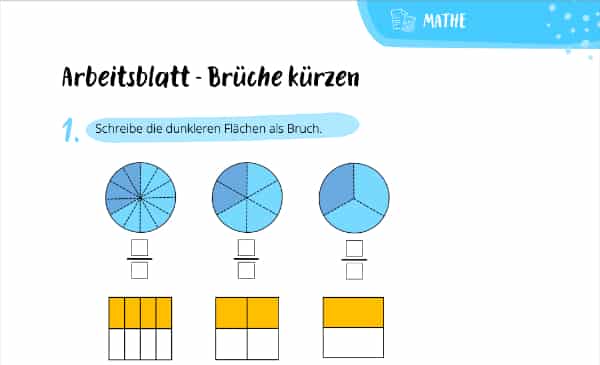
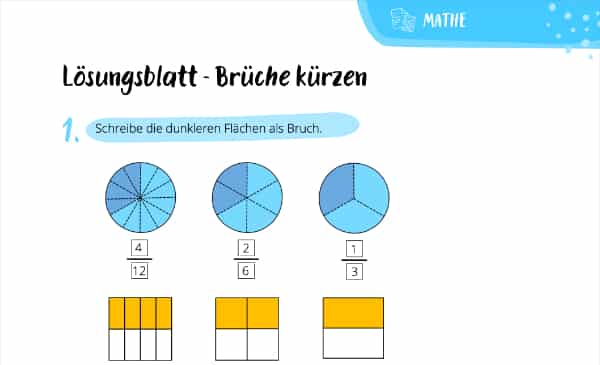
Wusstest Du, dass Dir Brüche kürzen das Leben erleichtert? Dazu musst Du nur die Zahl über und unter dem Strich durch dieselbe Zahl teilen. Wenn Du sie auf diese Weise vereinfachst, kannst Du nämlich viel besser damit rechnen. Praktisch, oder? Sollte Dir die Bruchrechnung noch nicht so leichtfallen, dann bringt Dich unsere Mathe Nachhilfe garantiert weiter!

Was bedeutet Brüche kürzen?
Brüche kürzen bedeutet, dass Du die Zahlen oberhalb und unterhalb des Bruchstrichs so weit wie möglich verringerst. Dabei musst Du aber keine Angst haben, dass plötzlich ein anderes Ergebnis beim Rechnen herauskommt. Du teilst schließlich den oberen (Zähler) und unteren (Nenner) Teil durch dieselbe Zahl. Damit bleibt der Wert an sich gleich, obwohl er anders aussieht. Man sagt dann, dass zwei Brüche gleichwertig sind.
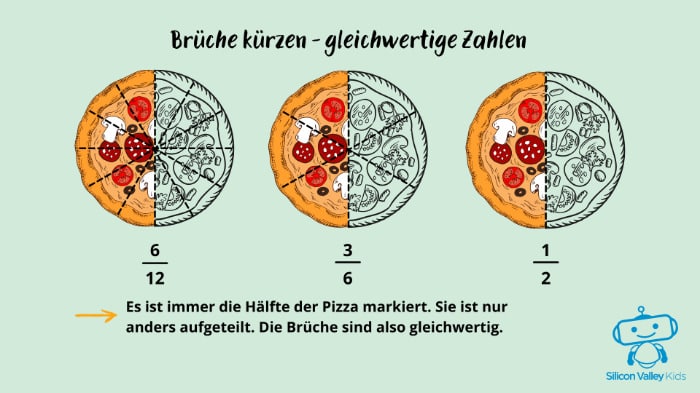
Wie kann man Brüche kürzen?
Beim Brüche Kürzen musst Du nur sowohl den Zähler als auch den Nenner durch einen gemeinsamen Teiler dividieren (vgl. Wartha / Padberg, 2017). Diesen gemeinsamen Teiler nennt man deswegen auch Kürzungszahl. Als Gegenoperation hierzu kann man übrigens Brüche erweitern.
Übrigens
Eine Zahl, mit der Du auf keinen Fall teilen kannst, ist die 0. Das ist in der Mathematik nämlich nicht erlaubt.
Durch dieselbe Zahl teilen
Wenn Du die Zahlen eines Bruchs durch dieselbe Zahl teilen kannst, hast Du auf jeden Fall eine Kürzungszahl gefunden. Dazu ist es hilfreich, zu wissen wie man Brüche dividieren kann. Wie genau das in der Praxis funktioniert, zeigt Dir folgendes Beispiel:
Aber Moment! Mit der 2 kann man zwar vereinfachen, aber die Aufgabe ist noch nicht ganz fertig. Du kannst nämlich noch einmal teilen:
Größter gemeinsamer Teiler
Sobald Du durch den größten gemeinsamen Teiler dividierst, erhältst Du direkt eine vollständig vereinfachte Bruchzahl. Das ist super, wenn Du beispielsweise zwei Brüche vergleichen sollst. An unserem Beispiel sieht das so aus:
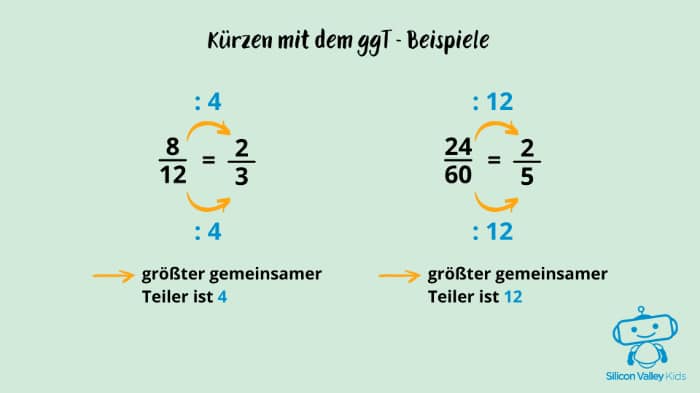
Lassen sich Brüche unendlich oft kürzen?
Eine Bruchzahl kann nicht unendlich oft gekürzt werden. Dabei weißt Du, dass Du fertig bist, wenn es keinen gemeinsamen Teiler mehr gibt. Man nennt den Nenner und den Zähler dann teilerfremd. Laut der Universität Siegen ist das der Fall, wenn der größte gemeinsame Teiler 1 ist.
Arbeitsblatt zum Kürzen von Brüchen
Jetzt hast Du bestimmt einiges dazugelernt. Wusstest Du, dass die Bruchrechnung für viele Schüler:innen gar nicht einfach ist (vgl. Dürrschnabel et al., 2019)? Nachdem Du unser Arbeitsblatt gelöst hast, gehörst Du bestimmt nicht mehr dazu. Viel Spaß!
Das war doch gar nicht schlimm, oder? Jetzt macht Dir beim Thema Kürzen bestimmt keiner mehr etwas vor. Solltest Du noch etwas Unterstützung wollen, ist das auch kein Problem. Dafür ist unsere Nachhilfe für die Grundschule schließlich da!
Literatur
Dürrschnabel, Klaus et al. (2019): Bruchrechnen. In: So viel Mathe muss sein!. Springer Spektrum, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-57951-0_6.
Wartha, Sebastian / Padberg, Friedhelm (2017): Didaktik der Bruchrechnung. 5. Auflage, Deutschland: Springer Berlin Heidelberg.
FAQs zum Kürzen eines Bruchs
Das ist ein Thema, das in der 5. oder 6. Klasse behandelt wird.
Man kann sie nur vereinfachen, wenn sich der Nenner und der Zähler durch einen gemeinsamen Teiler dividieren lassen. Funktioniert das nicht, dann muss die Teilmenge stehen bleiben, wie sie ist.
Wenn Du vollständig kürzen möchtest, dann verwendest Du den größten gemeinsamen Teiler (ggT).
Beispiel: Aus wird durch die 4 (ggT) dann
. Du hättest auch durch 2 teilen können, aber dann hättest Du nicht vollständig gekürzt.