Schriftliches Addieren erkläre ich Dir in dem folgenden Artikel. Dabei lernst Du schnell große, aber auch viele verschiedene Zahlen zusammen zu rechnen. Die schriftliche Addition basiert darauf, die einzelnen Ziffern der beteiligten Zahlen einzeln zu addieren. Demnach ist schriftliches Addieren das Zusammenrechnen kleiner Zahlen. Ich zeige Dir, welche Besonderheiten es geben kann, worauf Du manchmal achten musst, aber auch, wie Du sehr große Zahlen, oder auch Kommazahlen schriftlich bewältigen kannst. All diese Grundlagen zeigen wir Dir auch ausführlich in unserer Mathe Nachhilfe. Lass uns loslegen!
Inhaltsverzeichnis
Schriftliches Addieren oder plus rechnen
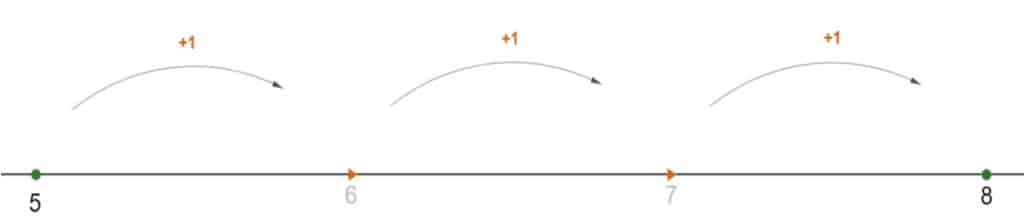
Bevor Du durch schriftliches Addieren so richtig in Fahrt kommst, möchte ich Dir nochmal erklären, was eine Addition eigentlich ist. Bei einer Addition werden zwei Zahlen miteinander addiert. Das bedeutet, dass Sie „zusammengerechnet“ werden, also, dass der Wert der einen Zahl zum Wert der anderen Zahl hinzugefügt wird. Nehmen wir das Beispiel 5 + 3. Wie Du sicher weißt, lautet das Ergebnis dieser Additionsaufgabe 8. Du kannst Dir Dies aber auch gut am Zahlenstrahl vorstellen, indem Du bei der 5 beginnst und von dort aus 3 Schritte nach rechts gehst.
Die Zahlen, welche addiert werden, heißen Summanden. Das Ergebnis wird Summe genannt. Dementsprechend sind bei der Addition 5 + 3 = 8 die Zahlen 5 und 3 die Summanden. Die Summe ist hier die Zahl 8.

Schriftliche Addition mithilfe von Einern, Zehnern und Hunderten
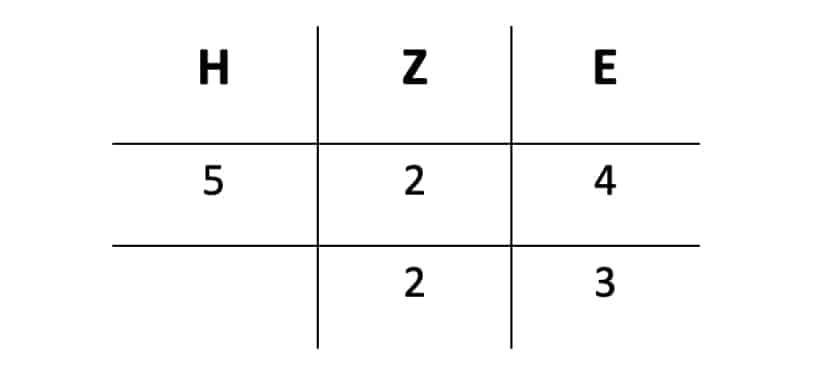
Schriftliches Addieren erfordert ein gewisses Maß an Vorwissen. Dabei weißt Du sicherlich schon, dass man jede ganze Zahl in Einer, Zehner, Hunderter usw. zerlegen kann. Du wirst gleich sehen, dass dies die Addition erheblich vereinfacht.Nehmen wir als Beispiel die Zahl 524. Diese hat 5 Hunderter, 2 Zehner und 4 Einer. Du kannst dies auch gut in einer Tabelle veranschaulichen.
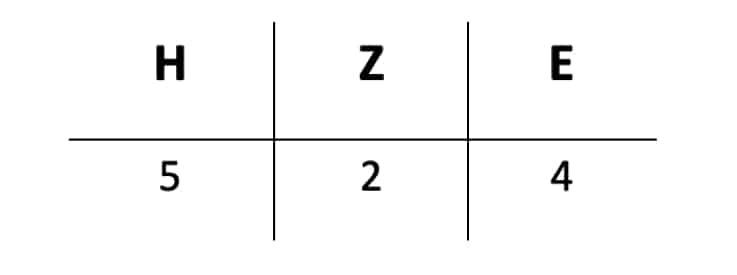
Ich möchte Dir nun zeigen, wie Du diese Zahl mit einer anderen Zahl schriftlich addieren kannst. Als Beispiel nehmen wir 524 + 23. Schreibe dazu die 23 ebenfalls in die Tabelle, indem Du 2 Zehner und 3 Einer einträgst.
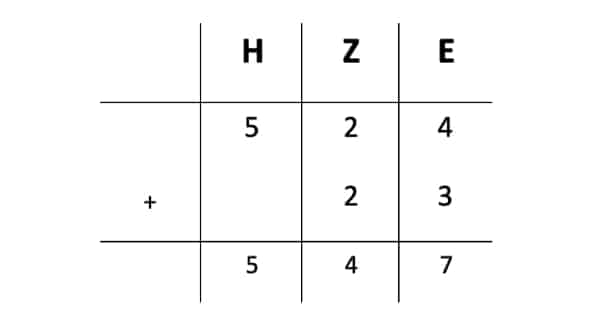
Für die schriftliche Addition brauchst Du jetzt nur die jeweiligen Spalten zu addieren (vgl. Gutjahr (2012)). Dies sieht dann wie in Abbildung 5 aus. So erhältst Du also Dein richtiges Ergebnis 547!
Mit Überschlag schriftlich Addieren
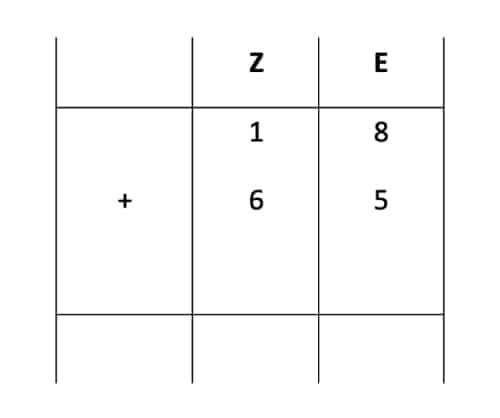
Ein wichtiger Fall beim schriftlich Addieren ist, dass eines Deiner Zwischenergebnisse nicht mehr nur als eine Ziffer dargestellt werden kann. Ich zeige Dir dies am Beispiel 18 + 65, wozu wir beide Zahlen wieder anhand der Tabelle zerlegen.
Du siehst, dass wir beim ersten Rechenschritt 8 + 5 = 13 haben, also mehr als eine Stelle. Dies ist aber kein Problem, denn Du kannst die 13 Einer wieder in Zehner und Einer zerlegen.
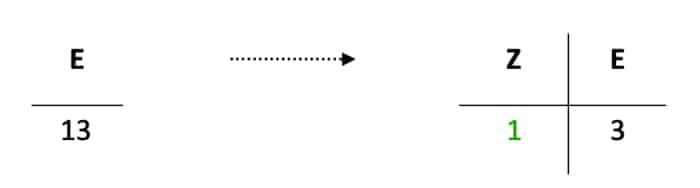
Danach schreibst Du die Einer unten in das Ergebnis und notierst diese von der Verschiebung auch bei den Zehnern in Deiner Rechnung, wie in Abbildung 8 veranschaulicht.
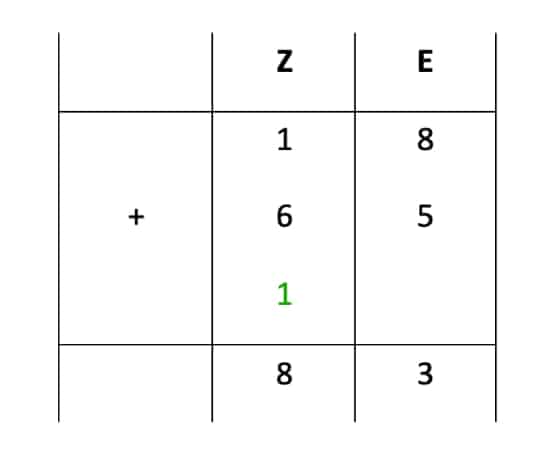
Um Dein Ergebnis zu erhalten, rechnest Du die übrigen Spalten wieder zusammen. Vergiss dabei bitte nicht die zusätzliche 1. Kommt so eine Verschiebung beim schriftlichen Addieren vor, so spricht man von einem Überschlag. Weitere Erklärungen zu diesem Thema findest Du in unserem Bereich Hausaufgabenbetreuung.

Warum unter den Rechnerverfahren schriftliches Addieren zu den wichtigsten gehört, kannst Du gerne der Universität Hamburg entnehmen.
Das schnelle Schema mit Beispiel
Nachdem Du die Grundlagen für die schriftliche Addition verstanden hast, möchte ich Dir ein einfaches und schnelles Schema beibringen. Damit lernst Du schnell, wie Du viele und auch große Zahlen addieren kannst (vgl. Keil (2011)). Ich zeige Dir dies am Beispiel 53 + 68:
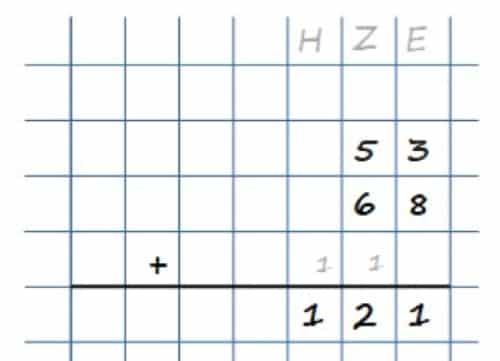
Du beginnst wie gewohnt rechts mit der schriftlichen Addition. Zwischen dem letzten Summanden und dem Ergebnisstrich lässt Du am besten ein Kästchen Platz.
Deine erste Rechnung lautet 3 + 8 = 11, also benötigst Du einen Überschlag. Im Schema kannst Du dies ganz einfach umsetzen: Schreibe die Einer Deines Ergebnisses dazu unten in das Ergebnis. In Deinem Fall also die hintere Eins von der 11. Den Überschlag, also die Zehner in Deinem Zwischenergebnis notierst Du dann mit einer kleinen Eins eine Spalte weiter links – in diesem Fall unterhalb der 6.
Anschließend gehst Du eine Spalte nach links und addierst 5 + 6 + 1 = 12 (denke an Deinen Überschlag). Wieder Zweistellig, aber das kannst Du ja schon! Notiere die 2 im Ergebnis und schreibe die 1 von der 12 in die nächste Spalte links. Dann berechnest Du noch die Summe der nächsten Spalte. Da hier nur eine Eins auftaucht, schreibst Du sie unten ins Ergebnis. Damit hast Du 121!
Unser Tipp
Um Deinen Mitschülern immer einen Schritt Voraus zu sein, solltest Du Dich auch schon einmal mit dem Thema schriftliches Multiplizieren befassen.
Mit 3 Summanden
Nachdem wir nun die Grundlagen besprochen haben, möchte ich Dir das Schema anhand eines etwas größeren Beispiels zeigen. Wir nehmen hierzu 524 + 38 + 45:
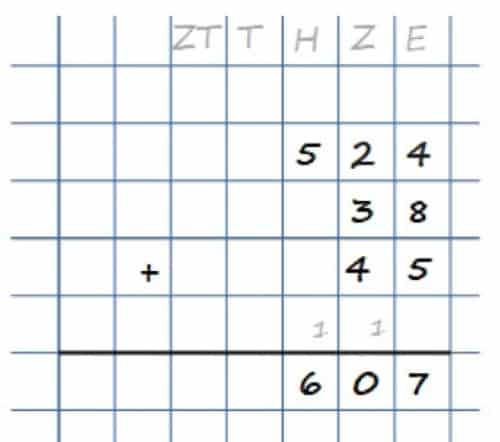
Wir beginnen wieder hinten und berechnen dort 4 + 8 + 5 = 17. Notiere also die 7 unten und den Überschlag 1 eine Spalte weiter links in das freie Kästchen. Dann haben wir 2 + 3 + 4 + 1 = 10. Schreibe also eine 0 unten in das Ergebnis sowie den Überschlag in die Spalte mit den Hundertern. Dort berechnen wir noch 5 + 1 = 6 und erhalten als Ergebnis 607!
Mit 5 Summanden
Nun bist Du fast schon ein Vollprofi! Lass uns daher nun eine große Aufgabe rechnen. Wir nehmen hierzu die Additionsaufgabe 8521 + 3438 + 745 + 460 +67:
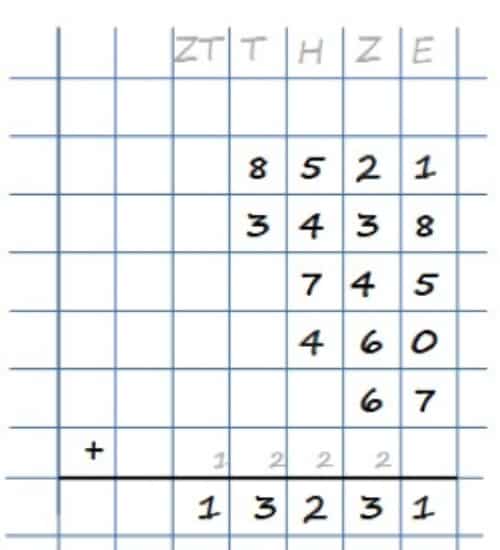
Beginne wieder rechts und berechne 1 + 8 + 5 + 0 + 7 = 21. Hier notierst Du wieder die Einer, also die 1 und schreibst den Überschlag 2 in das freie Kästchen eine Spalte weiter links oberhalb des Striches. Dann berechnest Du 2 + 3 + 4 + 6 + 6 +2 = 23 und trägst die 3 im Ergebnis sowie den Überschlag von 2 wie gewohnt ein. In der nächsten Spalte berechnen wir wieder 5 + 4 + 7 + 4 + 2 = 22. Trage die 2 ins Ergebnis Deiner schriftlichen Addition sowie eine 2 als Überschlag ein.
Danach berechnest Du 8 + 3 + 2 = 13. Also haben wir eine 3 im Ergebnis sowie einen Überschlag von 1. Als letzten Schritt erhältst Du also noch eine 1 bei den Zehntausendern. Schriftliches addieren all Deiner Summanden ergibt also das Ergebnis 13231!
Übrigens!
Die Reihenfolge bei der Addition darf immer vertauscht werden. Deswegen empfehle ich Dir die großen, also mehrstelligen Zahlen, immer oben und die kleinen unten auszuführen.
Weitere Informationen über die schriftliche Addition (sowie weitere mathematische Lösungsansätze) kannst Du gerne mal bei der Universität Potsdam nachlesen.
Schriftliches Addieren mit Kommazahlen
Mithilfe des obigen Schemas gelingt es Dir auch auch problemlos, die Summe aus Kommazahlen zu bilden. Du weißt sicher, dass auch die Stellen hinter dem Komma Bezeichnungen wie Zehntel, Hundertstel usw. haben. Achtest Du beim schriftlichen Addieren darauf, diese stets untereinander zu schreiben, so kannst Du die Addition wie gewohnt umsetzen.Ich zeige Dir nun, wie dies an einem konkreten Beispiel funktioniert. Schriftliches Addieren von Kommazahlen erkläre ich Dir nun am Beispiel 546,65 + 8,795.
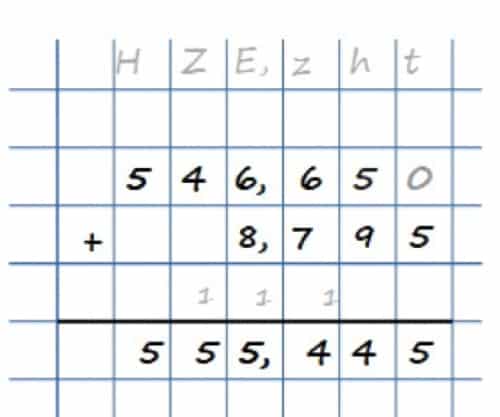
Als Hilfe kannst Du gerne die Zehntel (z), Hundertstel (h) sowie Tausendstel (t) oben in Deinem Schema ergänzen. Dazu ist es auch sinnvoll, wenn Du die Stelle des Kommas markierst – auch im Ergebnis! Da der erste Summand keine Tausendstel besitzt, kannst Du als Übersicht auch eine Null (wie oben in grau) ergänzen.
Für die Berechnung gehst Du wie gewohnt vor: In der hinteren Spalte hast Du 0 + 5 = 5. Danach rechnest Du 5 + 9 = 14, also notiere eine 4 im Ergebnis und eine 1 als Übertrag. Dann hast Du 6 + 7 + 1 = 14. Notiere also eine 4 und eine 1 als Übertrag. Links vom Komma haben wir dann 6 + 8 + 1 = 15, also im Ergebnis 1 und als Überschlag eine 1. Danach erhältst Du einmal 4 + 1 = 5 und zuletzt die 5. Das Ergebnis lautet also 555,445.
Eine Übersicht als Hilfestellung
Bevor wir zum Ende kommen, möchte ich Dir noch eine Zusammenfassung zur schriftlichen Addition geben, sodass Du nochmal alles in Ruhe überblicken kannst.
Tabelle 1: Schriftliche Addition Übersicht
| Addition | Beispiele | Bemerkung |
| Ohne Überschlag | 123 + 45 | Addition einzelner Ziffern führt zum richtigen Ergebnis |
| Mit Überschlag | 99 + 12 | Richtiges Übertragen von Zwischenergebnissen notwendig |
| Von Kommazahlen | 12,5 + 3,13 | Verfahren analog zu den obigen Fällen, solange die einzelnen Ziffern gemäß der Struktur untereinander stehen |
Additionsaufgaben
Da Du nun genug theoretisches Wissen erworben hast, ist es an der Zeit, das Gelernte in die Praxis umzusetzen. Bist Du denn bereit? Wir haben für Dich den Bereich schriftliches Addieren Aufgaben eingerichtet, in dem Du Dich ordentlich austoben kannst. Du willst noch mehr üben? Dann schau bei unserer Kinderbetreuung in Berlin vorbei! Die nächste Mathearbeit meisterst Du sicherlich mit Bravour!
Schriftliches Addieren kannst Du einfach und schnell mithilfe des Schemas lernen. Dieses hilft Dir übrigens auch beim Kopfrechnen üben. Beachte dazu, dass alles immer strukturiert untereinander steht. Dann kommst Du zum richtigen Ergebnis, sobald Du spaltenweise addierst und den Überschlag richtig notierst. Damit gelingt Dir mit diesem Schema auch die schriftliche Addition von Kommazahlen problemlos. Wichtig ist, dass Du schriftliches Addieren regelmäßig übst und Dein Wissen vertiefst. Gerne auch mit unseren Aufgaben und Lösungen. Der nächste Schritt wäre schriftlich subtrahieren. Wenn Du schon ein richtiger Vollprofi bist, empfehlen wir Dir, dass Du Dich auch schon einmal mit dem Bereich schriftliches Dividieren auseinandersetzt.
Literatur
Gutjahr, Sabine: Schriftliche Rechenverfahren (2012): Differenzierte Übungsmaterialien zur Addition, Subtraktion, Multiplikation und Division (3. und 4. Klasse). Lichtenau: AOL-Verlag.
Keil, Marion (2011): Lernstationen Mathematik: Schriftliche Addition: 3. und 4. Klasse. Buxtehude: Persen Verlag, 2011.
FAQs – Schriftliches Addieren
Um Dein Ergebnis zu prüfen, hast Du viele Möglichkeiten. Beispielsweise kannst Du einen der Summanden von der Summe subtrahieren. Kommt der zweiten Summand heraus, so kannst Du sicher sein, dass Du die schriftliche Addition richtig gerechnet hast. Demnach ist sie auch eine gute Möglichkeit, die schriftliche Subtraktion zu üben.
Du solltest einfache Additionsaufgaben bereits lösen können, denn bei der Schriftlichen Addition kommt es genau darauf an. Da beim schriftlichen Addieren aber auch viele kleinere Zahlen addiert werden, ist dies ebenfalls eine gute Möglichkeit das Addieren insgesamt zu vertiefen.
Die schriftliche Addition ist faszinierend einfach und schnell umzusetzen, sodass viele Menschen im Alltag, die viel rechnen müssen, immer noch gerne darauf zurückgreifen. Sei es der Kellner im Restaurant oder auch die Steuerberaterin. Sobald Du viele einzelne Zahlen addieren musst, bist Du mit der schriftlichen Addition sicherlich ähnlich schnell wie mit einem Taschenrechner.
Das ist ein gute Frage! Tatsächlich hängt das mit dem Stellensystem zusammen, denn die schriftliche Addition macht sich diese einfache Struktur zunutze. Falls Dir später in der Schule auch andere Stellensysteme, wie z.B. das Binärsystem, begegnen, so wirst Du sehen, dass auch dort eine einfache schriftliche Addition möglich ist. Computer rechnen so sogar jeden Tag!
An Deiner Sicherheit im Umgang mit der schriftlichen Addition. Sobald Du alle Aufgaben richtig gelöst hast, und auch sonst in der Lage bist, schnell und sicher auch mehrere Summanden zu addieren, dann bist Du außer Zweifel auf einem guten Weg!