Brüche subtrahieren

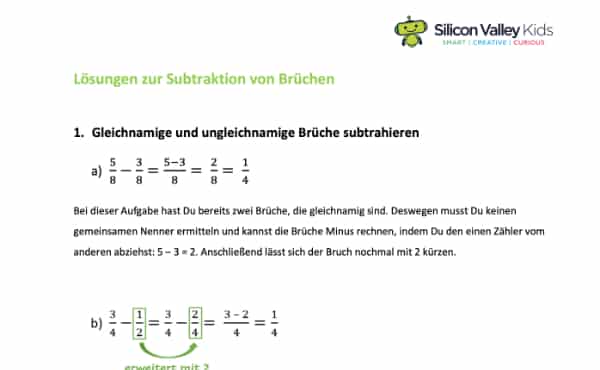
Falls Du Brüche subtrahieren willst, solltest Du das Plusrechnen der Bruchzahlen schon beherrschen. Um sie voneinander abziehen zu können, ist es jedoch manchmal notwendig, sie zu kürzen oder zu erweitern, wofür Du die Zähler und Nenner malnehmen oder teilen musst. Wenn Du Brüche Plusrechnen kannst, wird das Subtrahieren von Brüchen ein Kinderspiel für Dich sein! Solltest Du noch Fragen haben, zeigen wir Dir zudem in unserer Mathe Nachhilfe gerne alle Rechenregeln.

Im alltäglichen Leben Brüche subtrahieren

Es gibt viele alltägliche Situationen, in denen Du Brüche subtrahieren musst. Immer, wenn Du Anteile von einem Ganzen oder einem anderen Anteil entfernst, musst Du Brüche Minus rechnen. Die Grundvorstellung des Wegnehmens oder das Bestimmen eines Unterschieds (z.B. ein Vorher-Nachher-Vergleich) ist hilfreich, um zu verstehen, wie schriftliches Subtrahieren funktioniert (vgl. Padberg, 2017).

Nehmen wir an, dass Du noch $\frac 7 {8}$ einer Pizza hast und $\frac 2 {8}$ davon isst. Du möchtest jedoch Deinen Freunden auch etwas abgeben. Weißt Du, wie viele Anteile Du anschließend noch übrighast? Das wollen wir uns nun genauer anschauen.

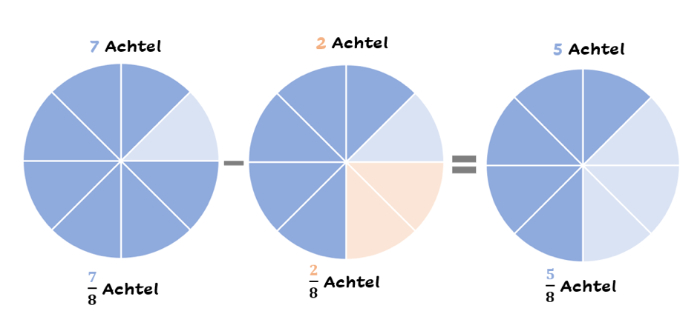
Brüche subtrahieren: Pizza aufteilen — *Abb. 1: Um eine Pizza aufzuteilen, musst Du Brüche subtrahieren*

Nachdem Du 2 Achtel von 7 Achtel der Pizza gegessen hast, bleiben Dir noch genau 5 Achtel übrig: D.h. Du kannst Deinen Freunden also $\frac 5 {8}$ der Pizza anbieten.

Brüche subtrahieren am Beispiel von Pizza

Bei diesem Rechenbeispiel konnten wir sofort subtrahieren, da die Brüche den gleichen Nenner hatten. Wann Du nicht sofort Minus rechnen kannst, möchte ich Dir deshalb jetzt erklären.

Info:

Brüche, die denselben Nenner haben, heißen gleichnamige Brüche: $\frac 7 {8}$ und $\frac 2 {8}$ sind demnach gleichnamig.

Welche Rechenregeln wir beim Subtrahieren von Brüchen anwenden, erläutere ich Dir anschließend ausführlich. Du willst die zuerst Grundlagen wiederholen? Dann schau Dir an, wie schriftliches Dividieren funktioniert.

Erklärvideo: Brüche subtrahieren

Am Zahlenstrahl einen Bruch subtrahieren

Wie man Brüche subtrahieren kann, möchte ich Dir nun mit einer anderen Darstellungsweise nochmal verdeutlichen. Um den Rechenweg zu veranschaulichen, nehmen wir dabei den Zahlenstrahl zu Hilfe. Denn die bildliche Darstellung auf einem Zahlenstrahl oder in Form von Anteilen an Kreisen hilft Dir dabei, Dir die Rechenaufgabe besser vorzustellen (vgl. Eichelmann et al., 2012).

Stell Dir vor, dass Du $\frac 7 {8}$ Liter Apfelsaft hast und von diesem $\frac 2 {8}$ Liter trinkst. Die volle Flasche enthielt dabei ursprünglich $\frac 8 {8}$ Liter. Anhand des Zahlstrahls kannst Du das auch gut sehen.

Brüche subtrahieren am Zahlenstrahl — *Abb. 2: Brüche mithilfe des Zahlenstrahls subtrahieren*

Unsere Aufgabe hierzu lautet: $\frac 7 {8} - \frac 2 {8} = \frac 5 {8}$ . Für $\frac 2 {8}$ gehen wir genau 2 Schritte auf unserem Zahlenstrahl zurück und gelangen so zur 5, also $\frac 5 {8}$ Liter. Nachdem wir also $\frac 2 {8}$ Liter von $\frac 7 {8}$ Liter Apfelsaft getrunken haben, sind noch genau $\frac 5 {8}$ in der Flasche.

Viele interessante Rechenaufgaben kannst Du Dir außerdem in der Publikation der Technischen Universität München anschauen.

Rechenregel für das Subtrahieren von Brüchen

Möglicherweise hast Du bemerkt, dass wir in beiden Beispielen mit Brüchen gerechnet haben, die den gleichen Nennern haben.

Aufgabe: $\frac 4 {5} - \frac 1 {5} = \frac {4-1} {5} = \frac 4 {5}$

Vielleicht ahnst Du bereits, welche Rechenregel dahintersteckt. Denn bei gleichnamigen Brüchen darfst Du die Zähler sofort subtrahieren. Dabei rechnest Du die beiden Zähler einfach Minus und behältst den gemeinsamen Nenner.

Merke:

Du subtrahierst gleichnamige Brüche, indem Du den gemeinsamen Nenner behältst und den zweiten Zähler vom ersten Zähler abziehst: $\frac 3 {5} - \frac 1 {5} = \frac {3-1} {5}$ .

Bei ungleichnamigen Brüchen ist das aber nicht so einfach, denn hier darfst Du diese Rechenregel nicht gleich anwenden. Bei einer solchen Aufgabe (z.B. $\frac 3 {8} - \frac 1 {7}$ ) musst Du die Bruchzahlen erst durch Erweitern oder Kürzen gleichnamig machen und auf einen Hauptnenner bringen.

Rechengesetze beim Brüche Subtrahieren

Rechengesetze helfen Dir geschickter und einfacher zu rechnen. Bei der Subtraktion gilt dabei das Distributivgesetz (Verteilungsgesetz). Dieses Rechengesetz ist wichtig, wenn eine Malrechnung zusammen mit einer Minusrechnung erscheint. Das Distributivgesetz beschreibt den Zusammenhang einer Punktrechnung (Malnehmen oder Teilen) mit einer Strichrechnung (Plus oder Minus rechnen) und man bezeichnet diesen Zusammenhang als distributiv (vgl. Krauthausen, 2006).

Du kannst die folgende Aufgabe einmal ohne die Anwendung des Rechengesetzes rechnen:

Aufgabe: $\frac 1 {2} \cdot (\frac 2 {3} - \frac 1 {3}) = \frac 1 {2} \cdot (\frac {2-1} {3}) = \frac 1 {2} \cdot \frac 1 {3} = \frac 1 {6}$

Oder Du wendest das Verteilungsgesetz an und löst hierfür die Klammern auf, indem Du jede Zahl mit dem Bruch vor der Klammer malnimmst. Rechne dabei Punkt vor Strich, d.h. die Malaufgaben zuerst und dann die Minusaufgabe.

Verteilungsgesetz: $\frac 1 {2} \cdot (\frac 2 {3} - \frac 1 {3}) = \frac 1 {2} \cdot \frac 2 {3} - \frac 1 {2} \cdot \frac 1 {3} = \frac {1 \cdot 2} {2 \cdot 3} - \frac {1 \cdot 1} {2 \cdot 3} = \frac 2 {6} - \frac 1 {6} = \frac 1 {6}$

Übrigens gilt das Distributivgesetz auch für schriftliches Addieren, wenn sich eine Plusaufgabe in der Klammer befindet.

Die Schmetterlingsmethode

Hauptnenner ermitteln und Bruch subtrahieren

Sobald die Brüche unterschiedliche Nenner haben, müssen wir sie gleichnamig machen, bevor wir sie anschließend Minus rechnen dürfen.

Merke:

Den Hauptnenner bildest Du, indem Du beide Brüche so erweiterst, dass sie den gleichen Nenner haben. Man nennt dies auch „gleichnamig machen“.

Damit wir wissen, mit welcher Zahl wir den Bruch erweitern oder kürzen, müssen wir das kgV (kleinstes gemeinsames Vielfaches) oder den ggT (größter gemeinsamer Teiler) ermitteln. Je nach Aufgabe lohnt es sich, entweder den Bruch zu erweitern oder zu kürzen. Deshalb möchte ich Dir jetzt zeigen, wie Du das rechnen kannst.

kgV bei der Subtraktion von Brüchen

Dabei Brüche gleichnamig zu machen, hilft Dir das kleinste gemeinsame Vielfache (kgV). Wir suchen den Hauptnenner, indem wir prüfen, welche Vielfachen die Nenner gemeinsam haben.

Demnach ist das kleinste gemeinsame Vielfache von 2 und 3 die 6, denn die 6 ist einerseits ein Vielfaches von 3 und andererseits ein Vielfaches von 2. Anders formuliert: 6 ist sowohl durch 2 als auch durch 3 teilbar.

Info:

Das kleinste gemeinsame Vielfache (kgV) ist die kleinste Zahl, die sowohl ein Vielfaches der einen Zahl als auch der anderen Zahl ist.

Der Hauptnenner ist beispielsweise die kleinstmögliche Zahl, die sowohl vom Nenner des einen als auch vom Nenner des anderen Bruchs ein Vielfaches ist.Nehmen wir einmal an, Du hast $\frac 1 {3}$ und $\frac 1 {2}$ in einer Aufgabe, dann ist 6 der Hauptnenner der beiden Nenner 3 und 2.

Der gemeinsame Nenner von $\frac 1 {3} = \frac 1 {2}$ ist 6.

Falls Du diese Brüche Minus rechnen willst, musst Du sie gleichnamig machen, indem Du sie auf den Nenner 6 erweiterst. Dafür erweiterst Du $\frac 1 {3}$ mit 2 und $\frac 1 {2}$ mit 3.

$\frac 1 {3} = \frac 2 {6}$ und $\frac 1 {2} = \frac 3 {6}$

Wie Du richtig erweiterst, zeige ich Dir jetzt. Falls Du das Kürzen und Erweitern schon gut beherrschst, kannst Du die nächsten Abschnitte überspringen.

Erweitern und Brüche Minus rechnen

Nachdem Du das gemeinsame Vielfache zweier Brüche ermittelt hast, darfst Du sie entsprechend erweitern.

Merke:

Wenn Du einen Bruch erweitern willst, musst Du Zähler und Nenner mit derselben Zahl malnehmen.

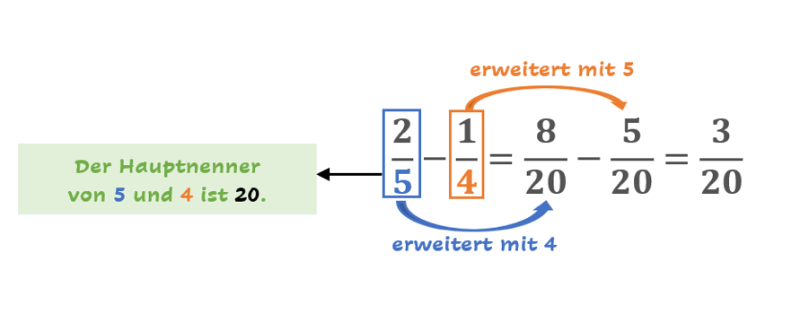
Du nimmst den Bruch dabei immer mit der Zahl mal, die den Nenner auf den gemeinsamen Nenner der beiden Brüche bringt. Zum Beispiel weißt Du, dass 20 der Hauptnenner von $\frac 2 {5}$ und $\frac 1 {4}$ ist und muss dann $\frac 2 {5}$ mit 4 erweitern bzw. malnehmen, da 5 ∙ 4 = 20 ist. Somit solltest Du immer prüfen, wie oft Du den Nenner malnehmen musst, damit er den Hauptnenner ergibt. Anschließend nimmst Du auch den Zähler mit dieser Zahl mal. Wie schriftliches Multiplizieren funktioniert, erfährst Du hier.

$\frac 2 {5}$ erweitert mit 4: $\frac {2 \cdot 4} {5 \cdot 4} = \frac {8} {20}$

Den anderen Bruch $\frac 1 {4}$ musst Du mit 5 erweitern, da 4 ∙ 5 = 20 ist. Sobald Du den Hauptnenner gebildet hast, kannst Du den Bruch subtrahieren.

$\frac 1 {4}$ erweitert mit 5: $\frac {1 \cdot 5} {4 \cdot 5} = \frac {5} {20}$

Gemeinsamen Nenner bilden — *Abb. 3: Bevor Du Brüche Minus rechnen kannst, musst Du sie auf einen gemeinsamen Nenner bringen*

ggT ermitteln beim Subtrahieren von Brüchen

Nicht immer ist es sinnvoll oder möglich, die Bruchzahlen durch Erweitern auf den gemeinsamen Nenner zu bringen. Deshalb nutzen wir manchmal lieber den größten gemeinsamen Teiler (ggT), um den Hauptnenner zu bilden.

Info:

Der größte gemeinsame Teiler (ggT) ist die größte Zahl, die sowohl die eine Zahl als auch die andere Zahl teilt.

Beim Teilen darf allerdings kein Rest bleiben. Demzufolge wäre die 4 der ggT von 12 und 24, da beide durch 4 teilbar sind:

12 : 4 = 3
24 : 4 = 6

Der Hauptnenner von $\frac {6} {12}$ und $\frac {18} {24}$ ist 4.

Du machst die Brüche gleichnamig, indem Du sie auf den Nenner 4 kürzt. Dafür kürzt Du $\frac {6} {12}$ mit 3 und zudem $\frac {18} {24}$ mit 6.

$\frac {6} {12} = \frac 2 {4}$ und $\frac {18} {24} = \frac 3 {4}$

Was Du beim Kürzen unbedingt beachten musst, zeige ich Dir anschließend im nächsten Abschnitt.

Gemeinsamen Nenner durch Kürzen bilden

Da Du nun weißt, wie Du den ggT ermittelst, wollen wir nun zwei Brüche durch Kürzen gleichnamig machen.

Merke:

Man kürzt einen Bruch, indem man Zähler und Nenner mit derselben Zahl teilt.

Du wählst dabei beim Teilen des Bruchs die Zahl, die Deinen Nenner auf den Hauptnenner bringt. Zum Beispiel weißt Du, dass 4 der größte gemeinsame Teiler von 32 und 24 ist. Somit ist 4 der gemeinsame Nenner von $\frac {16} {32}$ und $\frac {6} {24}$ .

Demzufolge musst Du $\frac {16}{32}$ mit 8 kürzen bzw. durch 8 teilen, da 32 : 8 = 4 ist. Du prüfst also, welche Zahl die 32 so teilt, dass sie den Hauptnenner 4 ergibt. Anschließend teilst Du auch den Zähler durch diese Zahl. Du kannst nur dann kürzen, wenn der Zähler und der Nenner durch dieselbe Zahl geteilt werden können.

$\frac {16} {32}$ mit 8 kürzen: $\frac {16 : 8} {32 : 8} = \frac {2} {4}$

Den anderen Bruch $\frac {6} {24}$ musst Du jedoch mit 6 kürzen:

$\frac {6} {24}$ mit 6 kürzen: $\frac {6 : 6} {24 : 6} = \frac 1 {4}$

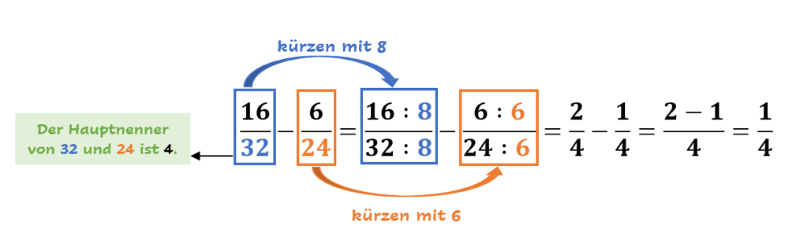
*Abb. 4: Beim Subtrahieren von Brüchen den Hauptnenner durch Kürzen bilden*

Durch das Kürzen kannst Du die beiden Brüche anschließend voneinander abziehen.

Brüche gleichnamig machen

Obwohl wir uns schon einige Beispiele angeschaut haben, wollen wir uns eine weitere Aufgabe ansehen und prüfen, wie man Bruchzahlen durch Erweitern und Kürzen gleichnamig macht.

Bei der folgenden Rechenaufgabe wollen wir dabei zunächst die erste Bruchzahl mit der Zahl 2 erweitern, um sie auf den Hauptnenner 16 zu bringen. Somit wird $\frac 3 {8}$ zu $\frac {6} {16}$ .

Aufgabe: $\frac 3 {8} - \frac {2} {16} = \frac {3 \cdot 2} {8 \cdot 2} - \frac {2} {16} = \frac 6 {16} - \frac {2} {16} = \frac {6-2} {16} = \frac 4 {16} = \frac 1 {4}$

Wir können den zweiten Bruch aber auch kürzen, um ihn auf den gemeinsamen Nenner 8 zu bringen. Demnach wird wird $\frac {2} {16} zu \frac 1 {8}$ .

Aufgabe: $\frac 3 {8} - \frac {2} {16} = \frac 3 {8} - \frac 1 {8} = \frac {3-1} {8} = \frac 2 {8} = \frac 1 {4}$

Subtraktion von unechten Brüchen

Da Du jetzt ungleichnamige Brüche subtrahieren kannst, wollen wir uns noch die Unechten anschauen. Wenn der Zähler größer als der Nenner ist, spricht man von einem unechten Bruch. Bei der nächsten Rechenaufgabe ist unser Hauptnenner 15, daher erweitern wir zunächst. Kurzum wir erweitern $\frac {20} {5}$ mit 3 und zudem $\frac {10} {3}$ mit 5.

Aufgabe: $\frac {20} {5} - \frac {10} {3} = \frac {60} {15} - \frac {50} {15} = \frac {60-50} {15} = \frac {10} {15} = \frac 2 {3}$

Da unsere unechten Brüche einfache Zahlen im Zähler hatten, konnten wir sie problemlos erweitern. Doch haben wir besonders geschickt gerechnet? Grundsätzlich müssen wir meist mit unechten Brüchen rechnen, doch in diesem Fall hätten wir den Ersten auch in eine ganze Zahl und den Zweiten in einen Gemischten umwandeln können.

Aufgabe: $\frac {20} {5} - \frac {10} {3} = \frac 4 {1} - \frac {10} {3} = 4 -3 \frac 1 {3} = \frac 2 {3}$

Wie man im Bereich Bruchrechnung Subtraktion mit gemischten Brüchen und ganzen Zahlen rechnet, zeige ich Dir deshalb nun.

Gemischte Brüche subtrahieren

Genau genommen, kannst Du gemischte Brüche ganz ähnlich Minus rechnen. Jedoch sollte der gemischte Bruch immer in einen unechten umgewandelt werden, bevor Du den Hauptnenner bildest.

Merke:

Gemischten Bruch umwandeln: Ganze Zahl • Nenner + Zähler:

$5\frac 1 {3} = \frac {(5 \cdot 3) + 1} {3} = \frac {16} {3}$ .

Nachdem Du den gemischten Bruch in einen unechten umgewandelt hast, kannst Du den Hauptnenner bilden und den Bruch subtrahieren.

Aufgabe: $3\frac 3 {5} - 1\frac 1 {5} = \frac {18} {5} - \frac 6 {5} = \frac {18 -6} {5} = \frac {12} 5 = 2 \frac 2 {5}$

Gemischte ungleichnamige Brüche subtrahieren

Nun wollen wir eine Aufgabe mit ungleichnamigen Brüchen rechnen. Jedoch musst Du auch hier als erstes die Gemischten in Unechte umwandeln. Danach bringst Du sie durch Erweitern auf den gemeinsamen Nenner. Erst dann kannst Du subtrahieren.

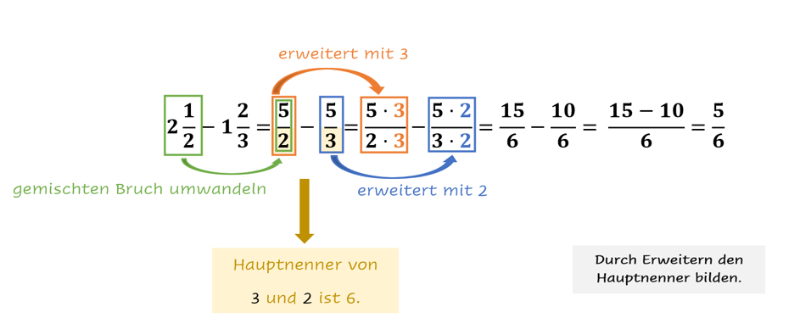
Gemischte Brüche Minus rechnen — *Abb. 5: Gemischten Bruch subtrahieren*

So subtrahierst Du gemischte Brüche:

Wandle zuerst den gemischten Bruch in einen unechten um.
Ermittle anschließend den Hauptnenner.
Bringe die Brüche durch Erweitern oder Kürzen auf den gemeinsamen Nenner.
Ziehe nun den Zähler des zweiten Bruchs vom Zähler des Ersten ab.

Dezimalbrüche subtrahieren

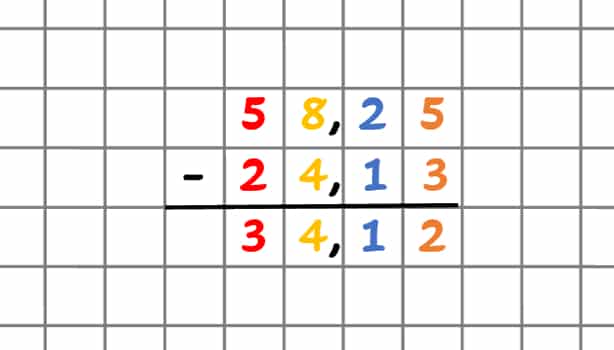
Die Regeln der schriftlichen Subtraktion helfen Dir beim Subtrahieren von Dezimalbrüchen. Dabei solltest Du darauf achten, dass die Kommastellen genau untereinanderstehen: Alle Stellen vor und hinter dem Komma müssen untereinander sein.

Wenn Du Dezimalzahlen subtrahieren möchtest, musst Du sie einfach untereinander schreiben und Dir das Komma wegdenken. Sobald Du das Ergebnis ermittelt hast, trägst Du die Kommastelle an der richtigen Position ein. Dabei musst Du lediglich die Kommastellen von rechts nach links zählen.

Dezimalzahlen Minus rechnen — *Abb. 6: Einen Dezimalbruch Minus rechnen*

Falls Du mehr zum Thema Dezimalbrüche erfahren möchtest, lies Dir Kapitel 3.3 der Veröffentlichung der Universität Siegen durch.

Brüche mit ganzen Zahlen subtrahieren

Zum Schluss lernst Du noch, wie Du Brüche mit ganzen Zahlen subtrahieren kannst. Anders als beim Plusrechnen, kannst Du Dir das Minuszeichen jedoch leider nicht wegdenken. Denn beim Subtrahieren müssen wir erst die ganze Zahl in eine Bruchzahl umwandeln. Allerdings ist das gar nicht schwierig.

Merke:

Eine ganze Zahl wandelst Du in einen Bruch um, indem Du 1 als Nenner nimmst und die ganze Zahl als Zähler schreibst: 4 = $\frac 4 {1}$ .

Nachdem Du eine ganze Zahl in einen Bruch umgewandelt hast, kannst Du wie gewohnt den Hauptnenner bilden und den Bruch Minus rechnen.

Aufgabe: $2- \frac 1 {3} = \frac 2 {1} - \frac 1 {3} = \frac {2 \cdot 3} {1 \cdot 3} - \frac 1 {3} = \frac 6 {3} - \frac 1 {3} = \frac {6-1} {3} = \frac 5 {3} = 1 \frac 2 {3}$

Diese Regel gilt selbstverständlich auch, wenn die ganze Zahl hinter dem Minuszeichen erscheint. Doch hier kannst Du die beiden ganzen Zahlen einfach voneinander abziehen und 5 – 2 rechnen.

Aufgabe: $5\frac 1 {3} - 2 = 3 \frac 1 {3}$

Übersicht der Rechenregeln

Um sicherzustellen, dass Du alle Rechenregeln für das Subtrahieren von Brüchen im Überblick hast, haben wir für Dich eine Tabelle erstellt. Denn hier siehst Du nochmal alle wichtigen Subtraktionsverfahren mit hilfreichen Rechenbeispielen.

Tabelle 1: Eine Übersicht, wie Du Brüche subtrahieren kannst

\frac 3 {8} - \frac 1 {8} = \frac {3 - 1} {8} = \frac 2 {8} = \frac 1 {4}

\frac 3 {4} - \frac 1 {2} = \frac {3 - 2} {4} = \frac 1 {4}

Übungsaufgaben & Lösungen

Nun solltest Du auch für das Subtrahieren von Brüchen fit sein. Deshalb kannst Du jezt mit unseren Übungen beginnen. Prüfe nun mithilfe unserer Arbeitsblätter, wie gut Du das Subtrahieren mit Bruchzahlen bereits beherrschst. Wir wünschen Dir dabei viel Freude! Falls Du noch mehr üben willst, dann sieh Dir an, wie Du Brüche multiplizieren kannst.

Download Aufgaben

Download Lösungen

Nun hast Du gesehen, dass das Subtrahieren von Brüchen kinderleicht ist. Sobald man den gemeinsamen Nenner durch Erweitern oder Kürzen gebildet hat, kann man die Zähler Minus rechnen. Falls Du die Subtraktion nun gut beherrschst, schau doch mal, ob Du Brüche dividieren kannst. Du willst Dich in Mathe weiter verbessern? Dann kannst Du Kopfrechnen üben.

Literatur

Eichelmann, A., Narciss, S., Schnaubert, L., Melis, E. (2012): Typische Fehler bei der Addition und Subtraktion von Brüchen – Ein Review zu empirischen Fehleranalysen. Journal für Mathematik-Didaktik, 33(1), 28-57.

Krauthausen, G., Scherer, P. (2006): Einführung in die Mathematikdidaktik. Heidelberg: Elsevier Spektrum Akademischer Verlag.

Padberg, F., Wartha, S. (2017): Didaktik der Bruchrechnung. Heidelberg: Elsevier Spektrum Akademischer Verlag.

FAQs – Brüche subtrahieren

Welche typischen Fehler machen Schüler, wenn sie Brüche subtrahieren?

Beim Subtrahieren von Brüchen vergessen Schüler oft, den Hauptnenner zu bilden und rechnen oft Zähler minus Zähler und Nenner minus Nenner: $\frac 5 {8} - \frac 2 {4} = \frac 3 {4}$ .

Wann lernen Schüler das Subtrahieren von Brüchen?

Das ist abhängig vom Lehrplan der Bundesländer. Allerdings lernen die meisten Schüler in der 5. oder 6. Klasse die Bruchrechnung. In einigen Grundschulen werden die Bruchzahlen jedoch schon in der 4. Klasse behandelt.

Kann ich drei Brüche subtrahieren?

Das kannst Du durchaus, allerdings musst Du alle Bruchzahlen auf den gleichen Nenner bringen. Anschließend kannst Du die Zähler wie gewohnt voneinander abziehen: $\frac 7 {8} - \frac 1 {4} - \frac 1 {2} = \frac 7 {8} - \frac 2 {8} - \frac 4 {8} = \frac {7-2-4} {8} = \frac 1 {8}$ .

Wann muss man im Alltag Brüche Minus rechnen?

Wenn Du einen kleinen Anteil von einem großen Ganzen oder einem weiteren Anteil wegnimmst, rechnest Du Minus mit Bruchzahlen: Du isst drei Viertel einer ganzen Pizza. Wie viel bleibt dabei übrig?

Wie bildet man beim Subtrahieren von Brüchen den Hauptnenner von 3 Nennern?

Bei folgendem Rechenbeispiel ist keiner der Nenner der Hauptnenner: $1\frac 1 {4} - \frac 1 {3} - \frac 1 {2}$ . Daher nehmen wir alle Nenner miteinander mal: 4 ∙ 3 ∙ 2 = 24. Zudem erweitern wir auf 24 und können die Brüche Minus rechnen: $1\frac 1 {4} - \frac 1 {3} - \frac 1 {2} = \frac 5 {4} - \frac 1 {3} - \frac 1 {2} = \frac {30}{24} - \frac {8} {24} - \frac {12} {24} = \frac {30-8-12} {24} = \frac {10} {24} = \frac 5 {12}$ .

Subtraktion	Beispiel	Bemerkung
Gleichnamige	$\frac 3 {8} - \frac 1 {8} = \frac {3 - 1} {8} = \frac 2 {8} = \frac 1 {4}$	Zähler der gleichnamigen Bruchzahlen subtrahieren.
Ungleichnamige	$\frac 3 {4} - \frac 1 {2} = \frac {3 - 2} {4} = \frac 1 {4}$	Brüche gleichnamig machen und anschließend die Zähler subtrahieren.
Bruch und ganze Zahl	$4 - \frac 2 {3} = \frac 4 {1} - \frac 2 {3} = \frac {12} {3} - \frac 2 {3} = \frac {10} {3} = 3 \frac 1 {3}$	Ganze Zahl in Bruch umwandeln, Brüche gleichnamig machen und dann Minus rechnen.
Dezimalbrüche	4,5 – 2,1 = 2,4	Schriftliche Subtraktion vornehmen und Komma setzen.
Gemischte	$1 \frac 1 {6} - \frac 1 {3} = \frac 7 {6} - \frac 1 {3} = \frac {7 - 2} {6} = \frac 5 {6}$	Gemischten Bruch in unechten umwandeln. Hauptnenner bilden und gleichnamige Bruchzahlen subtrahieren.