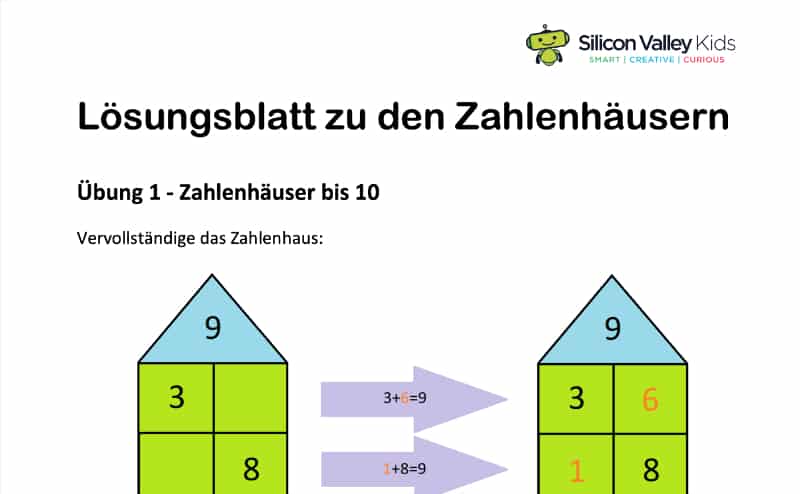
Hier erklären wir Dir, was Zahlenhäuser sind. Wenn Du gut aufpasst, wirst Du anschließend wissen, was diese Rechenaufgaben auszeichnet und wie sie Dir helfen, Dein Zahlenverständnis zu verbessern. Denn anhand von Zahlenhäusern lernst Du, in welche Teile eine Zahl zerlegt werden kann. Es wird Dir auf diese Weise nach und nach besser gelingen, Zahlen zusammenzurechnen. Solltest Du trotzdem noch Fragen haben, besprechen wir in unserer Mathe Nachhilfe gern alles ganz genau mit Dir.
Was sind Zahlenhäuser?
Zahlenhäuser sind Rechenaufgaben, die in Form eines Hauses dargestellt werden. Man nennt sie deshalb auch Rechenhäuser. Das Haus besteht hierbei aus einem Dach und mehreren Etagen. Im Dach steht eine Zahl, die als Dachzahl bezeichnet wird. Darunter befinden sich die Etagen, die jeweils aus zwei Zimmern bestehen. Stell Dir vor, dass in einem Haus immer nur die Zahlen auf einer Etage wohnen dürfen, die zusammen die Dachzahl ergeben. Beim Lösen wird deshalb jede Etage für sich betrachtet. Auf der Seite der Universität Osnabrück kannst Du zu dem Thema noch viel mehr spannende Dinge erfahren.
Beachte:
Obwohl ein Zahlenhaus mehrere Etagen hat, berechnest Du jede davon einzeln. Die Zahlen auf einer Etage müssen dabei zusammen so groß sein wie die Dachzahl.
Wie werden Rechenhäuser gelöst?
Zahlenhäuser kannst Du lösen, indem Du Dir die Dachzahl ansiehst und überlegst, welche Zahl in der jeweiligen Etage noch fehlt, damit beide Zahlen zusammen die Dachzahl ergeben. Sehen wir uns das nächste Beispiel deshalb einmal genauer an:
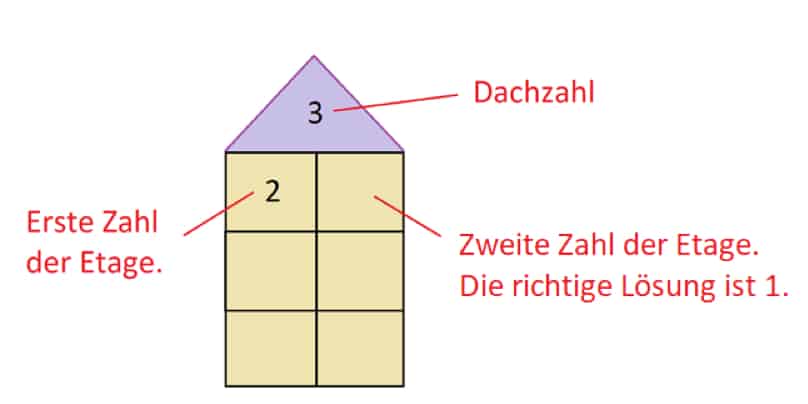
Im Dach des Zahlenhauses steht die Zahl 3. Du weißt jetzt schon, dass dies unsere Dachzahl ist. Unter dem Dach befinden sich drei Etagen. Jede Etage hat dabei zwei Zimmer. In der obersten Etage findest Du im linken Zimmer die Zahl 2. Um zur Lösung zu gelangen, musst Du Dir überlegen, welche Zahl wir im rechten Zimmer zur 2 dazurechnen müssen, um als Lösung die Dachzahl 3 zu erhalten. Die richtige Antwort ist die Zahl 1, denn 2 + 1 = 3.
Anhand eines Rechenhauses lernst Du deshalb, in welche Bestandteile sich Zahlen zerlegen lassen: Die Dachzahl 3 lässt sich in die Zahlen 2 und 1 zerlegen, deshalb befinden sich diese auf einer Etage (vgl. Harms, 2016).
Tabelle 1: Vorteile beim Rechnen mit Zahlenhäusern
| Struktur / Aufbau | Vorgehen | Vorteile |
| Zahlenhäuser sind wie echte Häuser aufgebaut. Sie haben mehrere Etagen und ein Dach. | Alle Zahlen einer Etage müssen zusammen die Dachzahl ergeben. | Durch die bildliche Darstellung lassen sich die mathematischen Zusammenhänge schnell verstehen. Die Verbildlichung hilft Dir außerdem, Dir das Gelernte besser zu merken. |
Zahlenhäuser bis 10
Lass uns mit dem Rechen anfangen. Auf dem nächsten Bild siehst Du ein Zahlenhaus mit Zahlen bis 10. Die Dachzahl erkennst Du schnell, es ist die Zahl 4. Jetzt schauen wir uns die oberste Etage an. Im linken Raum finden wir die Zahl 1. Im rechten Zimmer musst Du deshalb die Zahl herausfinden, die zusammen mit der 1 die Dachzahl 4 ergibt. Das richtige Ergebnis ist 3, denn 1 + 3 = 4. Andererseits kannst Du auch schriftliches Subtrahieren anwenden und von der Dachzahl 4 die 1 abziehen. Der Rechenweg sieht in diesem Fall so aus: 4 – 1 = 3. Keine Sorge, beide Wege führen Dich zum korrekten Ergebnis!
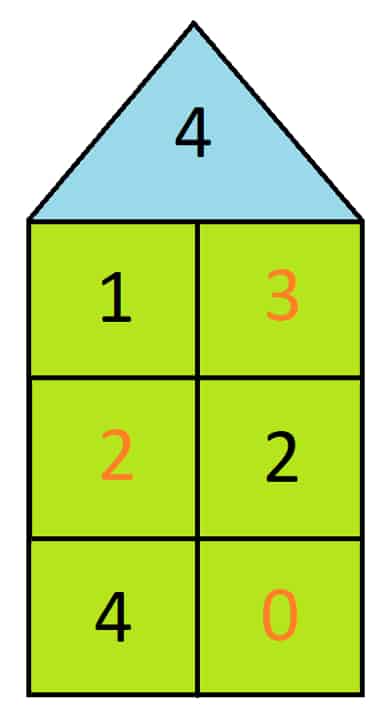
In der zweiten Etage ist die Zahl im rechten Raum vorgegeben, nämlich die 2. Also musst Du prüfen, welche Zahl zusammen mit der 2 die Dachzahl 4 ergibt. Die richtige Antwort ist die Zahl 2. Damit Du die Lösung besser erkennst, haben wir diese Zahl auf Abbildung 2 orange markiert.

In der untersten Etage steht im linken Zimmer eine 4. Es ist nämlich möglich, dass in einem Zimmer dieselbe Zahl steht wie im Dach. Natürlich müssen wir das leere Feld trotzdem weiter ausfüllen, wir dürfen aber nichts mehr dazurechnen. Deshalb gehört in das rechte Zimmer eine 0 als Ergebnis.
Rechenhäuser bis 20
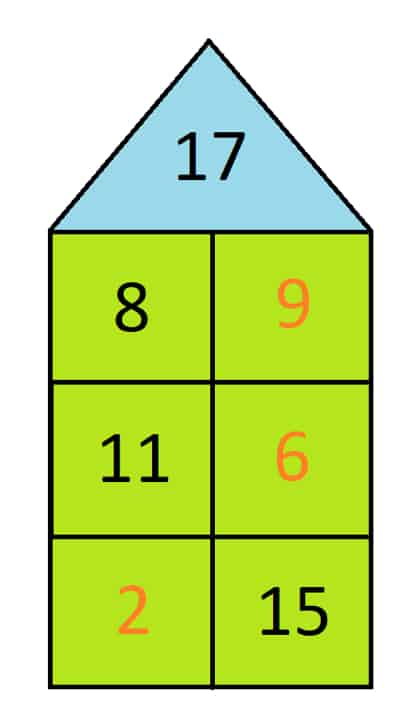
Ein Rechenhaus bis 20 erkennst Du daran, dass die Dachzahl bis zum Wert 20 gehen kann. Du bist bestimmt schon geübt in der Berechnung von Aufgaben in diesem Zahlenraum. Auf der nächsten Abbildung siehst Du ein Zahlenhaus mit der Dachzahl 17. Das Haus besteht wiederum aus drei Etagen. Die Ergebnisse der Rechenaufgaben haben wir wieder orange markiert. Lass uns gemeinsam die unterste Etage betrachten. Wir kennen die Zahl im rechten Zimmer, nämlich die 15. Das bedeutet, dass die Zahl im linken Zimmer so groß sein muss, dass in der Summe die Zahl 17 herauskommt. Du kannst Dich entweder fragen, wie viel noch von der 15 bis zur 17 fehlt oder Du ziehst von der Dachzahl 17 die Zahl 15 ab (vgl. Sinner, D., 2016). Bei beiden Varianten kommst Du schließlich zu dem Ergebnis, dass die Zahl im linken Zimmer der untersten Etage die 2 sein muss.
Zahlenhaus bis 100
Zahlenhäuser bis 100 sind schon schwieriger zu lösen. Wie Du Dir bestimmt bereits denken kannst, kann die Dachzahl nun Werte bis 100 annehmen. Dadurch musst Du natürlich auch anspruchsvollere Berechnungen durchführen. Wir sehen uns dieses Mal die mittlere Etage gemeinsam an. Die Dachzahl lautet 87. Auf der mittleren Etage ist die schwarze Zahl, die 13, bekannt. Deshalb ist es Deine Aufgabe, die Zahl im rechten Zimmer der mittleren Etage auszurechnen. Dazu kannst Du entweder schriftliches Addieren anwenden oder Minus rechnen. Wenn Du von der Dachzahl 87 die Zahl 13 aus dem linken Zimmer abziehst, erhältst Du die gesuchte Zahl 74, die Du in das rechte Zimmer auf dieser Etage eintragen kannst.
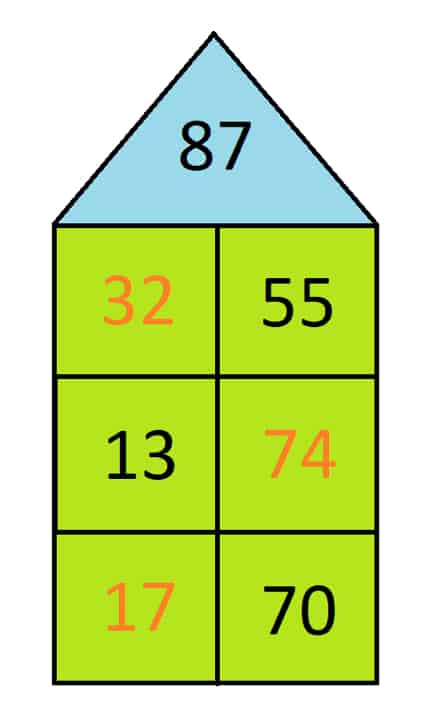
Und bist Du mitgekommen? Auch die unterste und die oberste Etage dieses Zahlenhauses haben es in sich. Wenn Du diese Rechnungen ebenfalls gelöst hast, kennst Du jedoch viele Beispiele für Zahlen, in die sich die 87 zerlegen lässt. Aber vergiss nicht: Das sind nur drei von vielen verschiedenen Möglichkeiten.
Beispiel für den Zahlenraum bis 1000
Rechenhäuser bis 1000 sind etwas für echte Mathe-Profis und so wie es aussieht, bist Du einer! Denn dieses Mal kann die Dachzahl sogar 1000 betragen. Das heißt natürlich auch, dass sogar die Zahlen der einzelnen Zimmer und Etagen sehr groß sind. Wir betrachten gemeinsam die oberste Etage unseres nächsten Beispiels. Die Zahl im linken Zimmer ist bekannt, sie lautet 547. Danach betrachten wir die Dachzahl, sie ist 786. Welche Zahl musst Du also zur 547 dazurechnen, damit 786 rauskommt? Die Lösung findest Du auf Abbildung 5. Rechenhäuser mit so großen Zahlen eignen sich übrigens sehr gut zum Kopfrechnen üben.
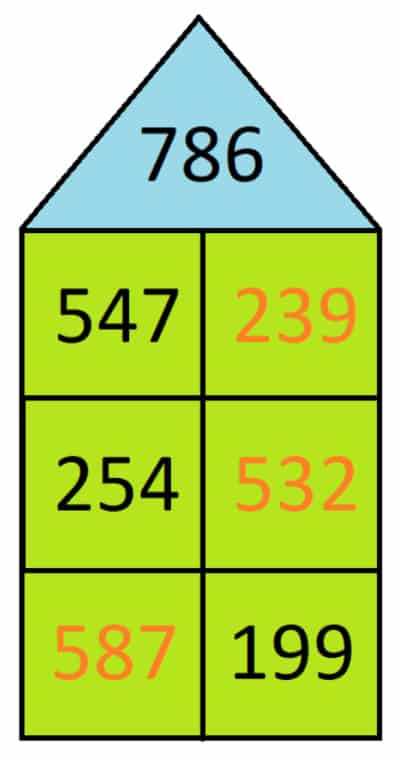
Die Dachzahl 786 ist so groß, dass es sehr viele Zahlenkombinationen gibt, aus denen man sie zusammensetzen kann. In unserem Beispiel haben wir dafür drei Möglichkeiten gefunden, nämlich die Zahlen auf den drei Etagen.
Rechnen mit dem Arbeitsblatt und Lösung
Du weißt nun, was Zahlenhäuser sind und hast mehrere Beispiele für diese Rechenaufgaben kennengelernt. Aber wir wissen: Übung macht den Meister. Deshalb haben wir für Dich Arbeitsblätter mit Rechenhäusern für die Zahlenräume 10, 20, 100 und 1000 erstellt. Damit kannst Du auch im Homeschooling weiter üben.
Zahlenhäuser eignen sich hervorragend, um ein besseres Verständnis für Zahlen und das Plus- und Minusrechnen zu bekommen. Je nachdem, wie gut Du schon in Mathe bist, kannst Du Dir die Größe und den Umfang des Rechenhauses aussuchen. In unserer Rubrik Hausaufgabenbetreuung findest Du zudem viele weitere Aufgaben.
Literatur
Sinner, D. (2016): Zählendes Rechnen überwinden – Zahlenraum bis 20. Leicht verständliche Handlungsanleitungen, praktische Übungen und Arbeitsblätter für Klasse 1., Auer-Verlag.
Harms, P. (2016): 18 Spiele zur Förderung mathematischer Kompetenzen – Mathematische Hürden spielerisch überwinden, Persen Verlag Hamburg.
FAQs – Zahlenhäuser
Um Zahlenhäuser zu lösen, kannst Du entweder die Zahlen auf einer Etage addieren oder auch die eine Zahl der Etage von der Dachzahl abziehen.
Rein theoretisch kann ein Zahlenhaus unendlich hoch sein und unendlich viele Etagen haben. Um solche Aufgaben zu bearbeiten, musst Du Dich jedoch schon mit Kommazahlen auskennen. Allerdings kannst Du auch mit ganzen Zahlen Rechenhäuser mit vielen Etagen bauen.
Welches Zimmer der Etage leer ist, spielt keine Rolle. Beim Plusrechnen kannst Du die Reihenfolge der Zahlen ändern, das Ergebnis bleibt trotzdem immer gleich.
Nein. Es gibt noch eine weitere Darstellung von Rechenhäusern, in der auch der Keller einbezogen wird, allerdings ist die Berechnung da etwas anders. Die meisten Rechenhäuser entsprechen den hier gezeigten Beispielen.
Ja, es gibt auch Zahlenhäuser mit denen Du schriftliches Multiplizieren und Dividieren üben kannst. Die Zahlen sind dann natürlich angepasst. Am häufigsten wird die Dachzahl jedoch durch das Plusrechnen ermittelt. Sollte ein anderes Rechenverfahren gefordert sein, wird darauf selbstverständlich hingewiesen.