Brüche vergleichen – im Nu verstehen

Wusstest Du schon, dass man Brüche vergleichen kann? Wie genau das funktioniert, erfährst Du hier. Außerdem klären wir, warum das in Zukunft ziemlich nützlich sein kann. Als krönenden Abschluss gibt es noch ein tolles Übungsblatt für Dich. Dir liegen noch ein paar Fragen auf der Zunge? Dann helfen wir Dir gerne in unserer Mathe Nachhilfe weiter!

Was bedeutet Brüche vergleichen?

Wenn Du Brüche vergleichen möchtest, musst Du entscheiden, ob sie größer, kleiner oder gleich groß sind. Gibt es bei Bruchzahlen etwa eine Körpergröße? Nein, das nicht. Aber Du kannst den Wert vergleichen, den sie darstellen. Welcher größer ist, hängt dann von den Zahlen der Nenner und Zähler ab. Das Sortieren wird einfacher für Dich, wenn die Nenner gleich sind. Ansonsten versuchst Du nämlich Zahlen zu vergleichen, deren richtige Werte Du gar nicht kennst.

Wie vergleicht man Brüche?

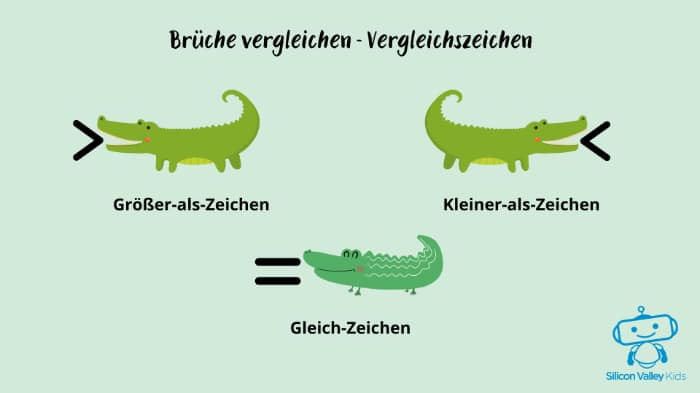
Brüche vergleichst Du, indem Du die Zähler unter die Lupe nimmst. Der Bruch mit der höheren Zahl über dem Bruchstrich ist dabei größer als der andere. Wenn Du ganz einfach aufschreiben möchtest, wie sie zueinanderstehen, hilft Dir die Mathematik weiter. Denn es gibt dafür drei mathematische Zeichen, die man Vergleichszeichen nennt. Das sind das Größer-als-Zeichen (>), das Kleiner-als-Zeichen (<) und das Gleich-Zeichen (=).

Gleichnamige Brüche

Bei gleichnamigen Brüchen ist es am einfachsten. Hier musst Du nur die Zähler vergleichen und das richtige Vergleichszeichen setzen. Lass uns einmal diese beiden Zahlen betrachten:

Die 5 im Zähler ist größer als die 2. Deswegen ist die erste Zahl größer als die zweite:

Bei gleichen Zählern

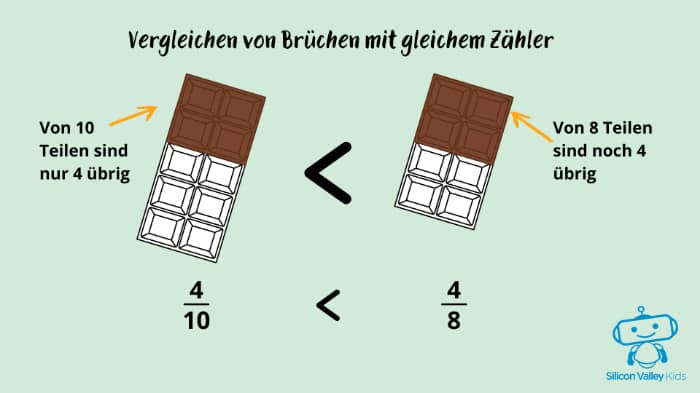
Manchmal können auch die Zähler statt der Nenner gleich sein. Dann gilt, dass der Bruch mit dem höheren Nenner kleiner als der andere ist. Das klingt erst einmal komisch. Aber erinnere Dich daran, dass der Zähler durch den Nenner geteilt wird. Wenn Du durch eine größere Zahl teilst, ist das Ergebnis automatisch kleiner. Am besten schauen wir uns mal ein Beispiel an:

Von den gibt es insgesamt 10 Teile, von denen noch 4 übrig sind. Bei den gibt es hingegen insgesamt 8 Teile und davon sind noch 4 Stück übrig. Jetzt sollte es etwas deutlicher sein, warum die kleiner als die sein müssen.

Wie kann man Brüche gleichnamig machen?

Das Vergleichen klappt besonders gut, wenn zwei Bruchzahlen gleichnamig sind, also denselben Nenner haben (vgl. Homrighausen, 2021). Eine Möglichkeit, sie gleichnamig zu machen, heißt Brüche kürzen. Dabei teilt man beide Zahlen am Bruchstrich durch denselben Wert. Du kannst ebenfalls Brüche erweitern, um den Nenner anzugleichen. Das funktioniert, indem Du Zähler und Nenner mit der gleichen Zahl malnimmst (vgl. Strobel, 2016).

Ungleichnamige Brüche vergleichen

Ungleichmäßige Brüche unterscheiden sich im Nenner und können zusätzlich unterschiedliche Zähler haben. Deswegen sollten sie auf jeden Fall angeglichen werden, bevor Du sie ordnest.

Wir erweitern die hier mit 3, sodass in beiden Nennern eine 21 steht:

Schon ist die Frage geklärt, welche Bruchzahl größer ist. Denn die sind größer als die :

Gemischte Brüche ordnen

Hier gestaltet sich das Vergleichen ein wenig kniffliger. Zuerst müssen diese Zahlen nämlich in normale Brüche umgeschrieben werden. Wir zeigen Dir an einem Beispiel, wie Du auch ihren Geheimnissen auf die Spur kommst.

Hinter der 1 verstecken sich hier , denn sie ergeben wieder 1 Ganzes. Dann bleibt noch übrig, das noch addiert wird:

Das heißt für unser Beispiel, dass beide Werte gleich groß sind.

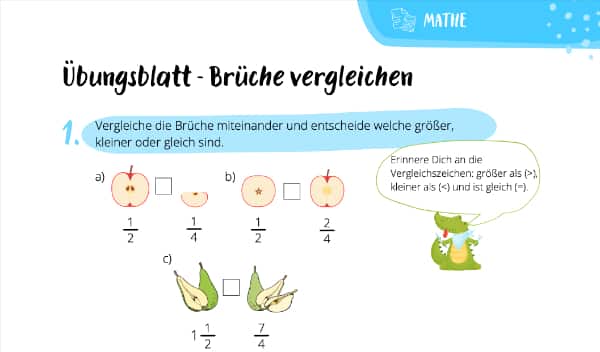
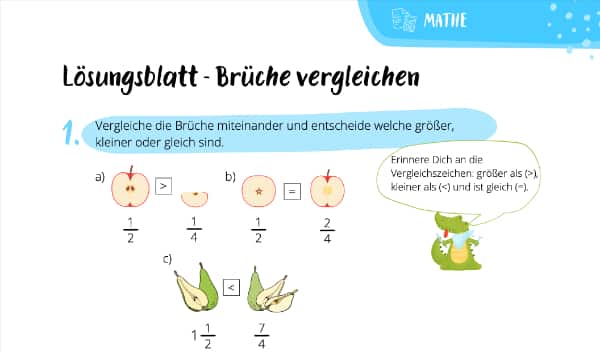
Übungsblatt zum Vergleichen von Brüchen

Genug Input von uns. Jetzt bist Du an der Reihe! Mit diesem Übungsblatt kannst Du Deinen Lernerfolg überprüfen und festigen. Viel Spaß dabei!

Wenn Du ab jetzt Brüche ordnen sollst, ist das bestimmt nicht mehr so schwierig für Dich, oder? Schließlich bist Du jetzt in alle hilfreichen Tricks eingeweiht. Sollte noch etwas unklar sein, kannst Du ja einfach noch einmal drüber lesen. Falls Du aber noch ein bisschen Unterstützung haben möchtest, sind wir mit unserer Nachhilfe für die Grundschule zur Stelle!

Literatur

Homrighausen, Heike (2021): Klett Ich kann … Mathe – Brüche und Dezimalzahlen 5./6. Klasse: Mathematik Schritt für Schritt verstehen. Deutschland: Klett Lerntraining bei PONS.

Strobel, Kerstin (2016): Bruchrechnung: Mathematik gemeinsam erarbeiten und begreifbar machen (5. und 6. Klasse). Deutschland: AOL-Verlag i.d. AAP LW.

FAQs zum Ordnen von Bruchzahlen